Decisive (but targeted, non-ubiquitous) election fraud occurred on November 3. What follows is an explanation and the evidence behind it.
- Starting in 1997, Smartmatic systems were developed in Venezuela with built-in functionality permitting precinct administrators to override security features it appeared to incorporate. Among the extraordinary privileges it gave administrators were abilities to:
- shave votes continuously from one candidate to another;
- batch ballots for later “adjudication” but which instead became a pool of votes that the administrator could simply assign to the candidate of choice;
- generate blank ballots.
- Through a series of licensing agreements, bankruptcies, and corporate mergers and acquisitions, that code ended up in various US election systems (e.g., Dominion, ES&S) which (branding aside) still derive from Smartmatic (a.k.a. Sequoia). Thus, they brought to US elections not only the generous functionalities permitting manipulation by administrators, but porous security, extending such powers to those abroad.[i]
- Since 2006 the fact that systems developed for Hugo Chavez were managing any US elections began striking some prescient Americans as unfortunate.[ii] Their trepidation was well-placed: on November 3, 2020 those systems were used strategically & aggressively to rig our election.
- It was strategic in that it was not “widespread” but targeted at six locations[iii] which, if flipped, also would flip the swing states in which they are found (and thus, the electoral college);
- It was aggressive for the simple reason that Trump broke their algorithm, because he was on his way to a win that exceeded their ability to overcome through minor cheats alone. It is for that reason that in those six locations the bad guys went full-on-goon (e.g., thugs intimidating observers, newspapers taped over windows, “water main breaks” shutting down counting then immediately reopened once Republican observers had departed, etc.)
- Three forms of evidence[iv] backing these claims dovetail perfectly;
- Documentation of extraordinary privileges Dominion provides administrators;
- Affidavits describing voters’ and workers’ experiences that match exactly what they would experience in precincts being gooned by the measures I describe;[v]
- Data (such as that below)[vi] expressing outrageous statistical oddities (e.g., strings of thousands of sequential Biden votes that occur with quadrillion-to-1 improbability, ballot processing velocity spikes that were physically impossible given available site equipment) that coincide with windows of intense intimidation of and interference with those observing the voting and counting.
- In each of several swing states Biden achieved a come-from-behind victory with a margin in the tens-of-thousands of votes thanks to getting hundreds of thousands of votes through these measures.
Conclusion: Election 2020 is an egg that can’t be unscrambled.
[i] By way of example:
- Dominions machines have glaring design flaws making them vulnerable to hacking. The machines have a slot on their motherboards that should be sealed with glue, but instead is left open: anyone with physical access to the machines can slide in the right chip for a few seconds, and that machine is thereafter completely compromised. In addition, there are R232 ports which would allow someone who accesses that port to connect and get root-level access to the machine without a password.
- Dominion’s uses solarwinds network software. On December 13, the US government pulled solarwinds off all federal networks due to its massive security vulnerabilities.
- Dominion’s servers are widely infected with QSnatch malware (see “CISA says 62,000 QNAP NAS devices have been infected with the QSnatch malware”, ZDNet, July 27, 2020). As poll-workers (e.g., administrators) log-in, QSnatch steals their credentials. Thus not only can administrators override (with no audit trail) election security in a precinct, so can anyone who steals those credentials (which, given the ubiquity of QSnatch on Dominion servers, happens everywhere). Dominion sends out software patches that continuously (deliberately?) allow QSnatch to beat their patches.
- Dominion uses SolarWinds networking software. On December 13, the federal government issued an emergency directive to all federal agencies to mitigate the profound network compromises brought by SolarWinds:

[ii] In a 2006 New York Times article (“U.S. Investigates Voting Machines’ Venezuela Ties”), Brad Golden wrote:
“The federal government is investigating the takeover last year of a leading American manufacturer of electronic voting systems by a small software company that has been linked to the leftist Venezuelan government of President Hugo Chávez. The inquiry is focusing on the Venezuelan owners of the software company, the Smartmatic Corporation, and is trying to determine whether the government in Caracas has any control or influence over the firm’s operations…”
In 2008, VoterAction (an activist group based in Massachusetts and Washington State) issued a public report (“SEQUOIA VOTING SYSTEMS, INC. USES VOTE-COUNTING SOFTWARE DEVELOPED, OWNED, AND LICENSED BY FOREIGN-OWNED SMARTMATIC, A COMPANY LINKED TO THE VENEZUELAN GOVERNMENT OF HUGO CHÁVEZ”) where they noted:
“U.S. national security is potentially at risk because software used to count votes in 20% of the country during U.S. elections is owned and controlled by a Venezuelan-run company with ties to the Venezuelan government of Hugo Chávez,1 which has been described as ‘the foremost meddler in foreign elections in the Western hemisphere.’2 Foreign-owned and foreign-run Smartmatic’s control over vote counting software used in the voting machines of Sequoia Voting Systems… presents a potential national security risk now just as it did in 2006 when the U.S. Committee on Foreign Investment in the United States (“CFIUS”) opened an investigation of Smartmatic’s ownership of Sequoia.3 CFIUS is a U.S. government inter-agency committee led by the U.S. Department of Treasury that addresses national security risks posed by foreign ownership of or influence over U.S. business, including companies providing the means by which voters in the U.S. elect their President and Congressional Representatives.4 Rather than answer to CFIUS regarding the ultimate owners of the Smartmatic conglomerate5 and its ties to the Chávez government, an investment group led by Sequoia management reportedly bought Sequoia from Smartmatic in late 2007 under terms that were not made public.6 Since then, however, it has come to light that Smartmatic continues to own the software that counts the votes on Sequoia voting machines and licenses to Sequoia that software, which Smartmatic develops in Venezuela.7 Concern, now, is that Smartmatic’s sale of Sequoia “was fraudulent”,8 “a sham transaction designed to fool regulators.”9 Efforts to date have not succeeded in determining the ultimate owners of Smartmatic or the extent to which Smartmatic and the Chávez government of Venezuela have influence over U.S. elections through Smartmatic’s control of the software that counts votes for Sequoia voting machines…”
See also this 2015 Philippines TV interview where Smartmatic’s chairman Mark Malloch-Brown (who, oddly enough, also serves as Vice-Chairman of George Soros’s investment fund and Open Society Institute) initially danced around such Venezuelan connections (note his oh-so-careful parsing of words in this regard) before eventually acknowledging a licensing arrangement between Dominion and Smartmartic.
[iii] Atlanta, Philadelphia, Detroit, Milwaukee, Maricopa County Arizona (Greater Phoenix), Clark County Nevada (Greater Las Vegas).
[iv] Due to my impatience waiting for these facts to bubble up through legal proceedings, and due to the extraordinary nature of the circumstances, I felt it was appropriate to create on article and get it live as soon as possible in order to make the Big Picture available to the public, then add charts and links and other evidence as time and opportunity allowed. As a result, I first posted this essay on the evening of Monday, November 23 and since then have been adducing further evidence since then. That way there will be one article that both tells the story succinctly, yet also gathers in one place much detail backing my claims.
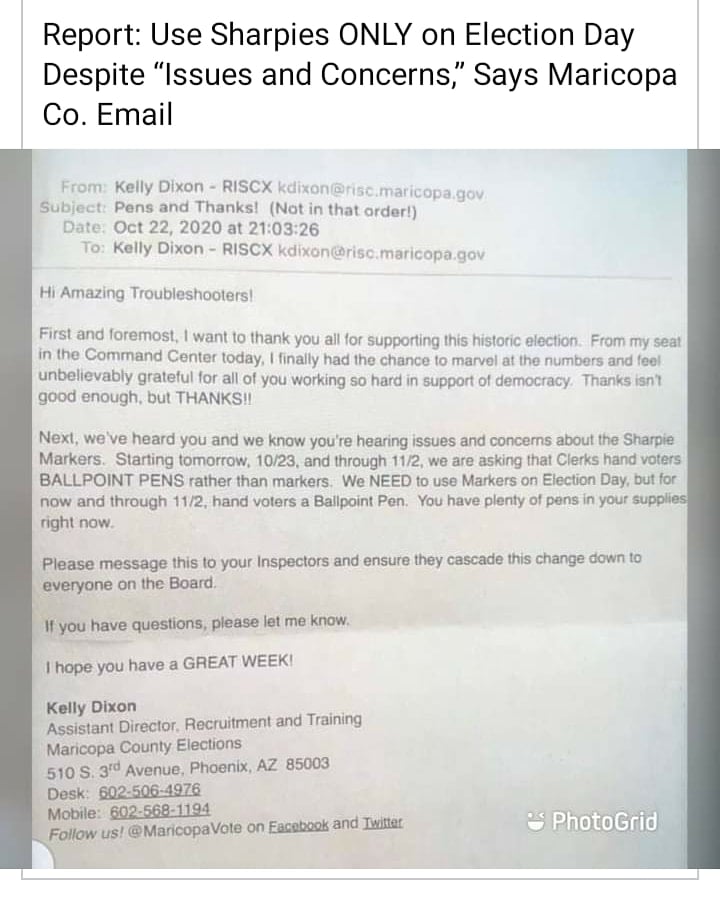
[v] By way of example: Sharpie/Bic switcheroos experienced in Maricopa precincts reflect a wish to generate a large pool of “adjudicated ballots” for administrators, who could drag-and-drop them later to Candidate Biden.
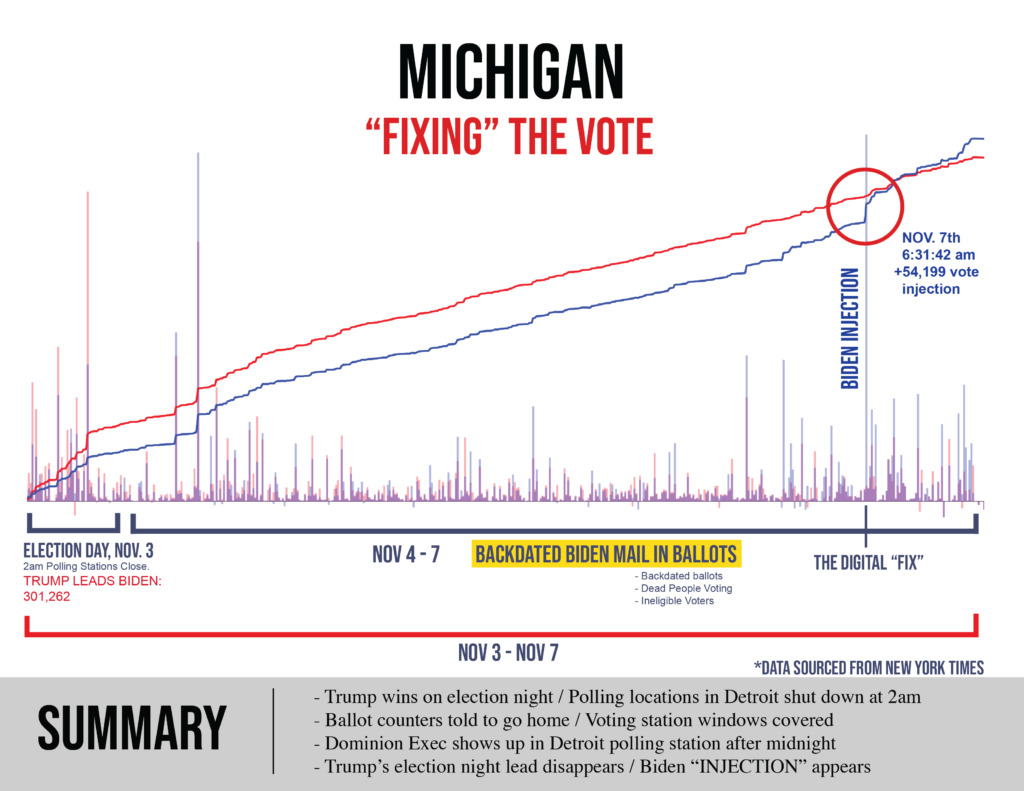
MICHIGAN
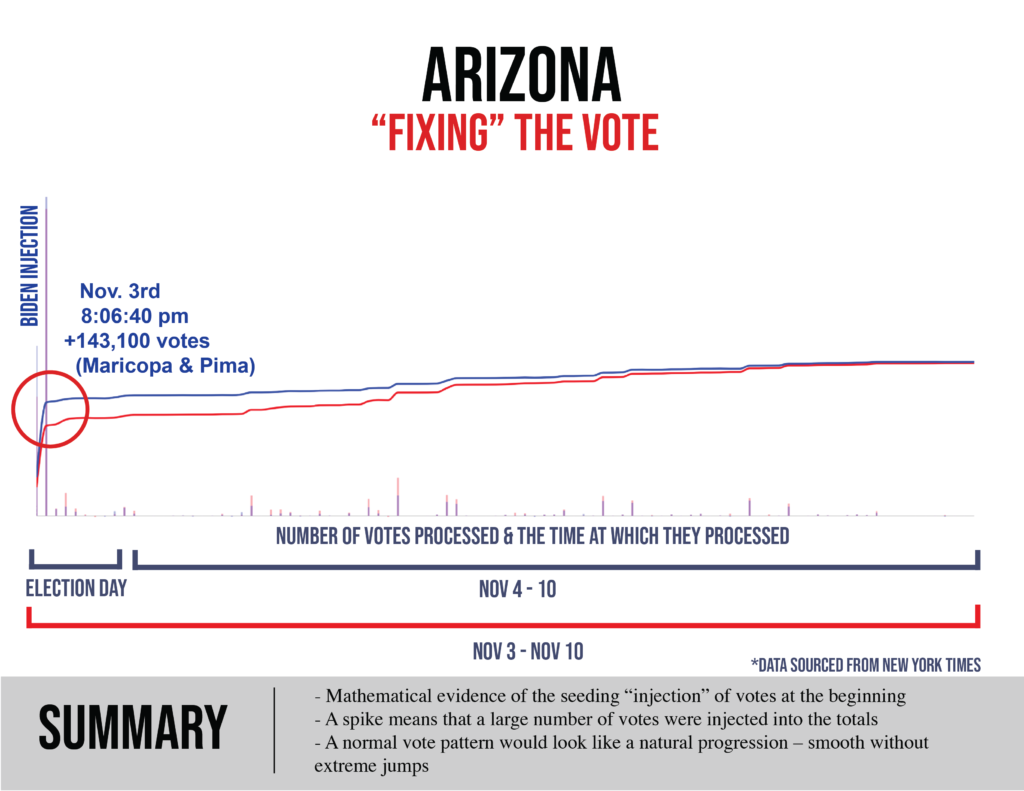
ARIZONA
GEORGIA
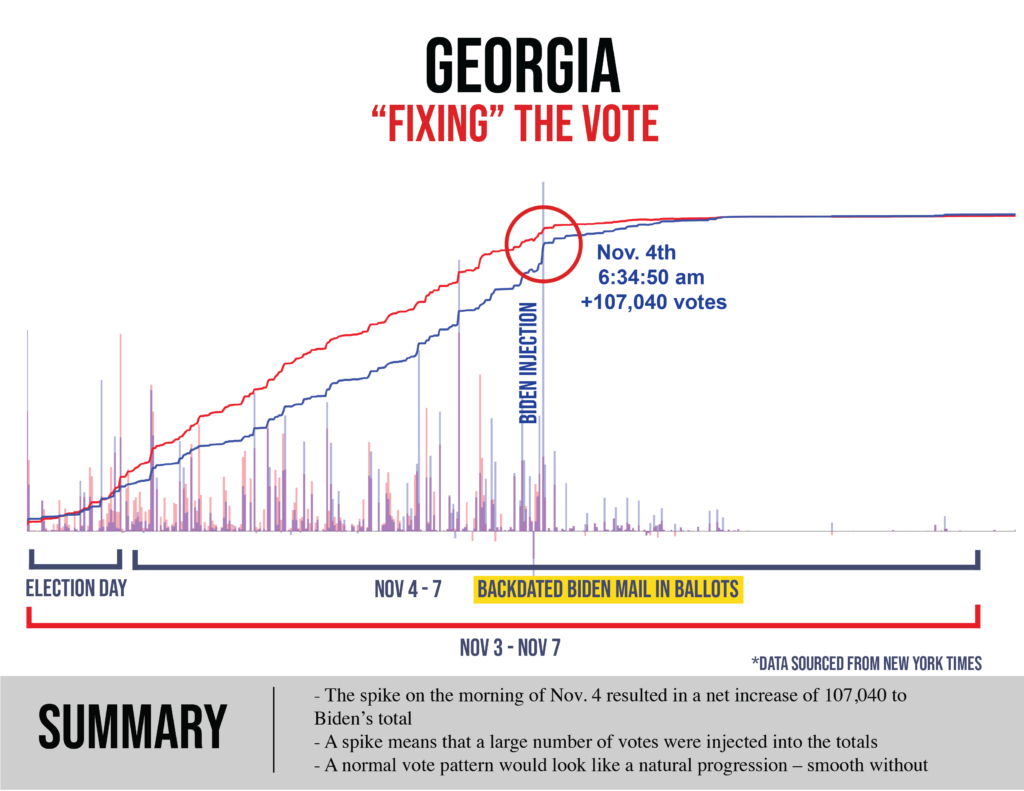
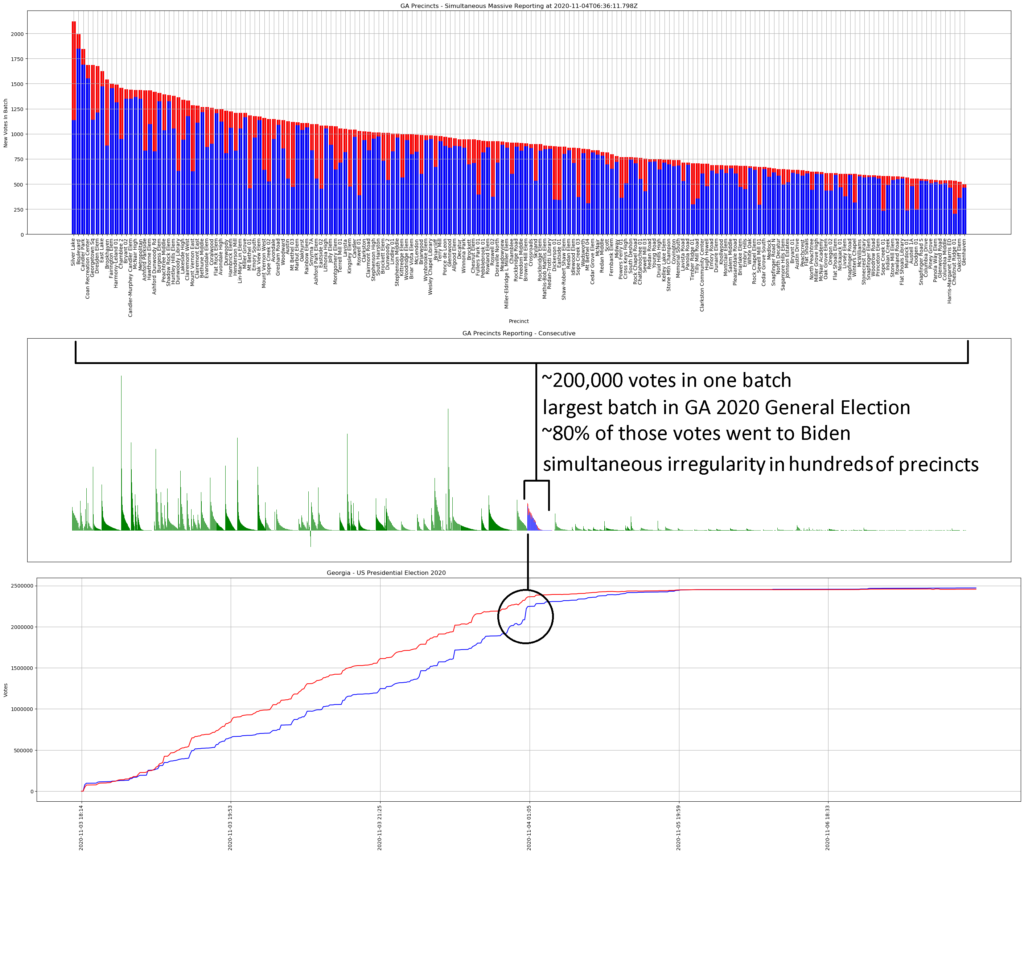
Election officials in Georgia have a history of quickly wiping their tracks: “APNewsBreak: Georgia election server wiped after suit filed” (AP, 10/2017).
Download this fine, heavily-documented affidavit from a Military intelligence analyst concerning Chinese, Iranian, and Russian penetration of Dominion Voting:Download











Thank you for this. I want to show this to people who still claim Conspiracy.. but a key piece of the article seems to be missing. “ charts (such as those below) seem to be missing, the article I’m reading does not show any charts below.?? I’m afraid to show people and have them say- where are the charts. Lol maybe I missed them.
Look I am a one-man show on DeepCapture. I posted a graph 5 minutes after I posted the text. 6-12 more graphs coming.
Hey man…thanks for doing what you can to help the cause for fair and decent elections. I’m just a dude who loves America, my wife, and God. Of course reverse that in order importance. I’m not rich…in fact disabled from a car wreck but if I can help somehow up in my section of the country let me know. Oh, I guess I should tell you I live in Port Orchard, WA. Near Seattle and I think Washington rigs their elections too. I want these crooked folks out of business. Later man.
Chris Pratt
[email protected]
Definitely need a recount now in GA since the shredder incident , also keep Stacey Abrams out .
Great Job Patrick you’re a true Patriot Sir
Thanks! Awesome work!
There is no actual proof of anything in these graphs…just stuff that average people who do not understand percentages and elections will jump to conclusions about.
The burden of proof is immense. Can we prove without a reasonable doubt that these tactics were indeed used. Is the mathematical irregularities enough to change courts minds? I really hope so, this is sickening, gut-wrenching, and our vote on Family pizza night is more accurate and honorable than this malarkey.!!! Time is precious, and the hill is a steep climb. I pray for America’s sake that everyone and their neighbors vote is legally counted. In my opinion, this disgusting scam started as soon as Hillary conceded and the phone was hung up! Courts NEED TO GET THIS RIGHT!!!!!!! Thank you from Maine for this very informative breakdown Patrick! Keep em coming so we the people can use our tongues to set forth the word.
Just to play Devil’s Advocate: the Michigan graph, while showing a vertical blue uptick on the right side of the chart, also shows a similar vertical RED uptick on the far left. Does this not weaken the case for Michigan? P.S. Amazing work regardless, and I hope and pray that justice prevails. With the entire media and the Deep State against us, this is as colossal a fight as one can imagine.
In the case of each of other spikes, both parties get a significant fraction of the votes. The end-of-count spike is the one that suddenly gives Biden a ton of votes with miniscule Trump vote.
I’m from Washington too. I have no doubt that they rig the elections here. We’ve been doing the cheat-by-mail system for a couple decades now and it’s time to get rid of it.
100% agree.
I live in Seattle, WA and I also agree 100%!!!
I’m in Washington. We need to press for election reform here. I’m very interested in seeing Culp’s lawsuit move forward. Here’s an article I’m working on. https://rlmartinwrites.com/2020/12/19/washington-state-allows-220-year-old-person-to-vote/
Patrick, you’re doing a great service to all patriotic Americans. Keep up the good work and keep fighting the good fight!
I live in Seattle, WA and I think the same too!!!
Hi Patrick, amazing work! Please do California next! Thank you for all your hard work!
I noticed that the affidavit from the Italian Tech that worked on the Satellites in Italy, where the ballots were sent to the servers and the Tech changed the algorithms when told to. That’s how Biden had so many votes more than President Trump. The servers were then sent to Frankfurt and the military supposedly had to gobthere to pick up the servers.
Patrick, I can’t tell you how welcoming your insight and info are at this point in time. I TRY not to look at msm and avoid the ones out there thinking I’m some kook who has cracked!!!! With everything in me, I feel – well, I all but knew it on the night of the 3rd. I’d put nothing past them to try, and lo and behold. But thanks to someone like you who has the ability and means to “dig for the good stuff” I so hope we can get the crimes revealed in time to get the RIGHTFULLY elected man back into office. Thank you…..
Barb
Great job Patrick! Keep it up! I’ll be referencing this page a lot.
Dear Patrick,
The future of our country hinges on the proofs of election fraud, and I salute your efforts and patriotic sacrifices in uncovering and analyzing those proofs.
My question is, will mathematical models and hypotheticals be sufficient for “proof” to carry the day in court, or will they be dismissed as “interesting statistical probabilities but not conclusively persuasive” evidence without DIRECT proof of say, discovering the electronic logs of the Smartmatic program in the questionable precincts or from wherever the program was controlled, and from that, showing that either a predetermined algorithm kicked in, or that a human(s) doing keystrokes (or inserting flash drives (or doing whatever they did) actually CAUSED the specific instances of vote changing, vote deletion, vote addition, etc.
In short, in a court of law, absent hard evidence of human intervention, does the mathematical / analytical theory — that is supported by expert statistical testimony and detailed analysis — stay just that, i.e., a “theory” that is hypothetically possible and quite interesting but unproven without
showing how, when, and where the humans did it ?
That is what I worry about.
God Bless, my friend.
Mike Rollo
Pensacola, FL
Member of the Florida Bar
With all due respect to your rather valid concern, is not the evidence set forth akin to proving arson without yet discovering who specifically set the fire?
Regardless, the fire destroyed the house and you have to start over.
Would it strictly be necessary to find he arsonist? In this case, the wrong that must be corrected is the fraudulent results, even if the parties responsible are never isolated and punished. You can correct one wrong without necessarily punishing the offenders individually.
You sir have hit the nail on the head. I will answer as best I can with the education I have recently received about courts of law.
Facts are what are proven in a trial. Here is where Sidney would have to prove actual voter fraud back up by hard facts. Not just statistics unless they were very compelling.
The SCOTUS does not decide facts, they answer constitutional arguments. “Most” cases must go to trial and work there way up to the SCOTUS..
BUT!!!!! There are a couple of cases, like Brown v. Board of Edu, where statistical data proved beyond a shadow of doubt that citizens rights were constitutionally violated.
There is more than enough statistical data to prove that Trump voters had their constitutional rights violated under the 14th Amendment. Chief Justus Roberts has argued this point in the past. This would cause the SCOTUS to throw out the election and then Congress would choose the Pres and VP.
There are super clear fraud patterns in the data stream as batches of data after the overnight count injections are frozen in the Biden Trump proportions MI WI GA VA.
The reported state level results show subtractions from Trump and additions to Biden, and deletions of Trump votes. How do you get a batch of negative ballot counts?
Gatewaypundit’s series “we caught them” has those tables
It is incontrovertible undeniably synthetic count.
For PA a more subtle clock rotation among precincts was used to hide the fixed ratios by distributing them.
You can partially back calculate the original votes from the state level data, but the ward/precinct level data will reveal much more, as the election interference was nationwide and as Dr. Shiva pointed out, it is more subtle and operated gradually on individual precincts by removing proportionally more Trump votes the higher the republican vote share was. He did a deep dive on MI, he may do more states.
The bottom line is that you can do the top level reversal of the manipulation and get a Trump win in PA MI WI GA VA. AZ was a simple dump during election day.
The future of the free world depends on good winning out over evil.
I am a patriot trapped in a Canadian’s body, I love my country but Trudeau has already destroyed it by siding with the evil that is the great reset also referred to as brainwashing the people and controlling them…seriously people this is where we are in history.
I can not believe the brazenness, SCOTUS can not ignore this or its game over.
Anything that’s forced on the people is not for the people.
Thank you and God Bless you for your information which I believe will help save our election process and our Country.
Please take care of yourself. “They” will be trying to stifle your voice and evidence.
It’s a shame that private citizens have to step up to do this kind of research because the Federal agencies charged with discovering and prosecuting crimes don’t do their jobs anymore.
Welcome to my life.
Sir, just a humble thank you from my family for what you and your team are doing! I do research if any assistance is needed. Just want to put it out there. I think (not proven) that Dominion has inside assistance when it comes to EAC certifications. If you look closely into Mr. Cobb who operates Pro V&V. Be happy to share more with you in a private email or conversation.
Thanks for the great work you are a true patriot. About the mail in ballots why doesn’t the Trump campaign jump on that right away ?
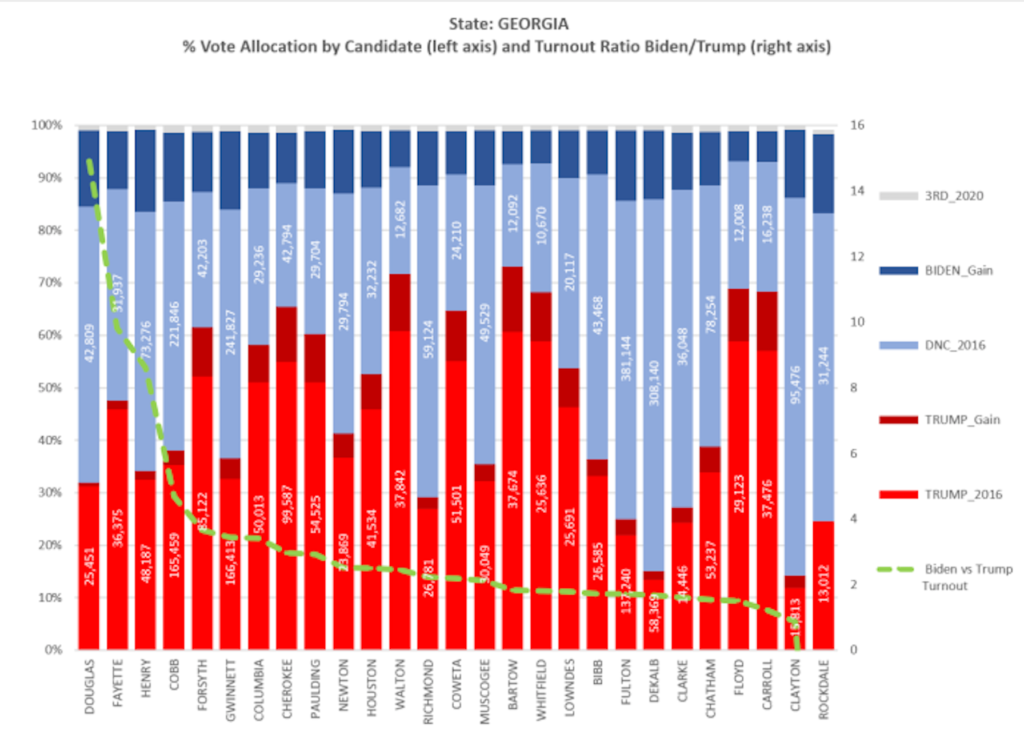
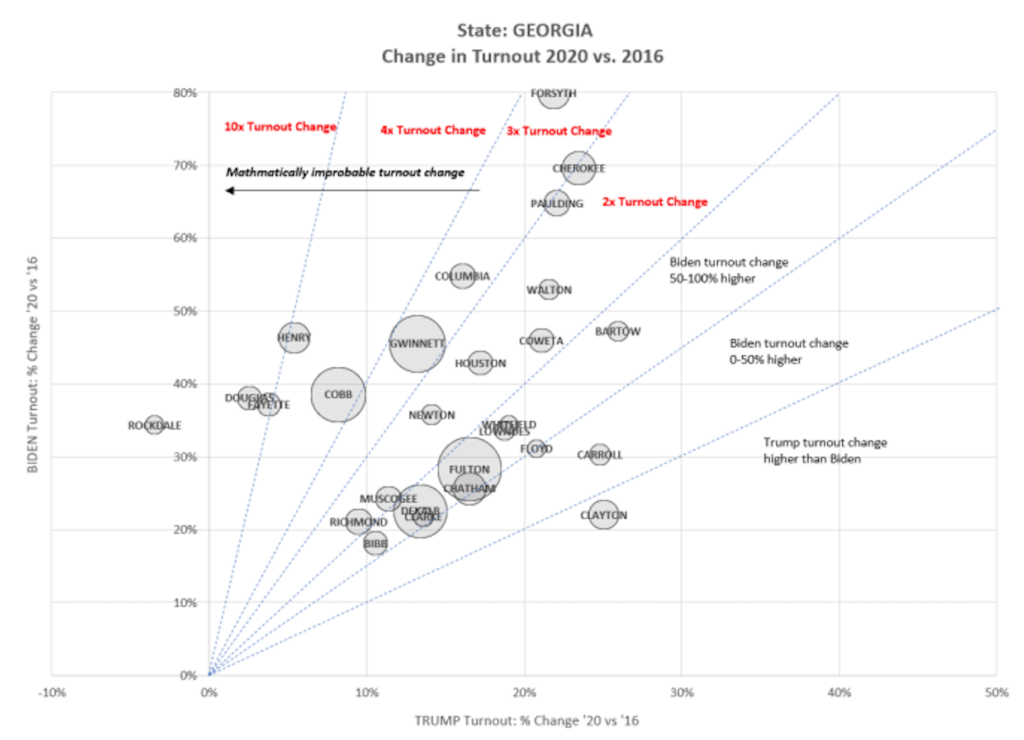
I’m confused by the green dotted line on the one Georgia graphic. What does the green line represent and what to the numbers on the right axis refer to? Numbers from 0 to 16 in increments of 2? The key says this is the Biden vs. Trump turnout ratio, but I’m not really sure what that means and it’s relevance?
Hopefully my answer helps.
At a high-level it says Douglas, Fayette, Cobb, Henry, Forsyth and Gwinnett counties have vastly different results in 2020 compared to 2016 relative to other Georgia counties. A ratio of 1 or close to 1 would say the 2020 & 2016 results are very similar or exactly the same. Is there a valid explanation or does the precinct level information make sense for these counties? Are there more whistle-blowers in these counties compared to other Georgia counties reporting voter irregularities? I don’t know the answer to these questions.
I believe the green-dot also says that Joe Biden outperformed Hillary Clinton in every county except Clayton county (unless the results change).
Comparing the 2016 results per county the green dot essential represents the difference between 2016 & 2020 total votes for Joe Biden compared to Donald Trump per county.
In Clayton county, Trump’s increase in 2020 vs 2016 votes was LARGER or better than Joe Biden’s 2020 vs Clinton’s 2016 vote increase. In 2016 Trump had 12645 votes compared to 15813 votes in 2020. A 25% increase of votes in 2020. However, Joe Biden received 95476 votes in 2020 compared to Hillary Clinton’s 78220 votes in 2016. A 22% increase. The green-dot line value slightly less than 1 or 22/25.
In Douglas county, Trump has 634 more votes in 2020 (25451) compared to 2016 (24817). Joe Biden has 11804 more votes in 2020 (42809) compared to 2016 (31005 Hillary votes). Trump’s votes increased by 2.6% but Joe Biden votes increased by 38% so the ratio is around 15 (38/2.6).
Please see Rockdale county in the chart right below the chart with the green dotted line. Trump’s 2020 vote total was 13012. His 2016 vote total was 13470. So Trump’s total votes in 2020 dropped by 3.4% in Rockdale. However, in Rockdale county Joe Biden’s total votes were 31244 compared to Hillary Clinton’s 23255 total votes in 2016- Joe Biden increased total votes by 35%. Seems like Rockdale county also has vastly different results in 2020 compared to 2016.
hello
You are a true patriot. Thank you!!!!
Its true smartmatic was used in the philippines thats why bonbong marcos was cheated by aquino and leni robredo as the false vp
Its true smartmatic was used in the philippines thats why bonbong marcos was cheated by aquino and leni robredo as the false vp
That is false. Leni Robredo actually gained more votes in the Presidential Electoral Tribunal recount.
Excellent article in my opinion. Check out Rumble and do a search on voter fraud. There are math experts posting charts and graphs all over the place such as the ones above!
Thank you God bless you Patrick. You are doing work the people like myself can’t.
I am truck driver from north dakota hauling crude oil. We so appreciate your help!!
hi Patrick, have you shared all these with Sidney Powell, Rudy Giuliani, and Lin Wood as they are fighting their cases?
Regardless of whether yours (and those of others) information gathering/sharing alter the publicly perceived/media promoted election results you have gained my respect and admiration for your efforts. If only for the sake of future elections it is imperative that the flaws/exploits in the current voting system(s) must be addressed in whole. One of the biggest challenges currently is every state, and every county within a state can, and in many cases do, have different methods, rules, and avenues to challenges any given election result(s).
The current system flaws have benefited both Republicans and Democrats over the course of time but I think the Republicans in whole may have made the decision that these flaws have become more of a liability than an asset during election cycles. IF this is the case hopefully they will support/sponsor wholesale election reform.
It boggles the mind that as a country we are openly touting our soon to be ability for space travel yet we lack the technology/ability to deploy a simple yet bulletproof voting system that would eliminate the shenanigans and vote stealing that IS NOT NEW but is only now being placed under a magnifying glass by many concerned citizens.
Please continue your efforts and know they are greatly appreciated.
I may have enjoyed reading your full post, but I’ll never know. I stopped when I arrived at your specious equivalence of “The current system flaws have benefited both Republicans and Democrats.”
Uniparty my friend. The Uniparty.
Republicans benefiting from this malicious activity were welcomed by Democrats with a wink and a nod, if not open arms.
This is what separates us from the left, we hold our own to account…the left only reinforces what each other is doing.
Take a look at vashiva.com website for a Republican fraud example.
Dr Shiva ran in the Republican Massachusetts primary and investing voter machine fraud since Sept. in his Republican primary. He is an expert witness for Powell, Trump, and his data is used by state legislatures. These lawsuits are uncovering potential very deep state/establishment fraud. CIA is even called out to. Just look at Russiagate and how many people were involved in other branches. The people spoke last time and establishment is under fire trying to squash the constitutional revolution. Dr Patrick and Dr Shiva are patriots and hope justice and truth prevail with these guys going in the history books saving our country!
Thank you so much for doing this! Blessings to you!
Thanks for your bravery and for putting you reputation on the line! Your a true american and i salute you sir!
Do you believe that there are votes being changed all over the country on smaller levels that help these democrat run cities like Portland keep winning. Useing the green button/steal.
Thank you for your courage. America needs to stand up and challenge all the BS the MSM and the tech companies are forcing feeding us. You sir are a patriot.
Thank you Patrick Byrne for your work saving our country. You may be the only man with the ability and willingness to expose this fraudulent election.
Patrick, my hope is that Sidney Powell, Lin Wood, and the Team team can utilize excellent analysis like this by you and others dedicating their time and effort to getting to the bottom of this obvious fraud. Thank you so much for your diligent work. You’re a true patriot.
However, looking beyond this deliberate fraud conducted by Democrat politicians and foreign actors working in concert, there’s the issue of a valid secure solution. I understand that you are, in part, a blockchain guy these days. Doesn’t it seem that this is the perfect opportunity and timeframe to create a secure, immutable, and transparent blockchain solution that makes it virtually impossible for anyone to cheat in any way? In my opinion, this is the only sure-fire solution that erases it from the possibility of happening again in the future? There would be some legal hurdles, but I think it needs to be done ASAP.
The most true statement here is you are a one man show. It is sad to see your desperate attempt to stay relevant after your super double agent spy story fell flat on its face. You went from respected business man and a colleague I respected to the store brand version of Rudy Giuliani. The graphs only show what everyone already knew, mail in voters were counted later and dems voted by mail. Why aren’t you talking about the Trump lead increasing in Arizona? Why aren’t you talking about suburban women voting against Trump? Why aren’t you talking about the down ballot Republican successes? Because it doesn’t fit your narrative. Charts can tell the story anyone wants to tell, surely your last CMO at Overstock taught you that? You used to like to be compared to George Washington and his leadership style. Let us do a better comparison and compare you to Benedict Arnold, a successful war hero that felt like he didn’t get adequate recognition so his ego led him to betray his nation. That is you, and that is Trump. It is no surprise you have a soft spot for Trump toxic narcissism and delusions of your own greatness are common traits between you. How far you have fallen and how said it is to watch. The fact you can’t believe that such a flawed, toxic, corrupt president would get 80 million votes against him demonstrates you don’t live in reality. Nobody will remember you, nobody will see you as a hero, you will be forgotten except to a handful of QAnon followers and Newsmax viewer. Sad. Pathetic. Heartbreaking. Disappointing
After horrible narcissistic Obama, Trump was a pleasure. Are you a Biden voter ? Might explain a lot. Did you vote for Hillary LOL.
Come on Justine, this election theft goes beyond the data trend anomalies (which are legit impossible), and into a multi faceted coup that was designed to guarantee a victory. If Biden/Harris had a scruple left to share, they’d be wanting this election to be fair and free. As it stands, more than half the voting citizens in this country do not trust the results and believe there were serious shenanigans that need to be addressed. Biden/Harris would do THEMSELVES and their potential win a favor by encouraging a decent investigation….or maybe they know something we don’t (that this election was stolen)?
Correction needs to be made The most true statement here is you are not a one man show. Thousands of others have undergone the same problems asking the same questions and getting same results. Nothing! Reasonable Doubt should start with evidence. However what happens when it won’t even be considered? When a Criminal act has been committed we’re told to report it to law enforcement. So what happens if they won’t except the complaint? It shunts the ability to start the legal process.
You are correct. A corrupt politician did get 80 million votes and his name is Joe Biden. The under the table scammer that has had his hands in the DC cookie jar for half a century. Sorry Justine, you apparently have a fascination with communism and the desire to be controlled. I have numerous friends who grew up fatherless due to the Biden segregationist and racist policies. His support of the crime bill so his kids did not grow up in a racial jungle. Well I did grow up in a jungle and it had everything to do with Bill Clinton and Joe Biden’s racist policies. I am off the plantation sister and we ain’t going back. Do you really think anyone believes that a candidate who could not get 20 people to a campaign “rally” and wears an adult diaper won the Presidency?
Well, aren’t you a cunt.
Whoa Billy Bob….watch the language please.
Spoken like a true marxist who probably believes everything the mainstream media rattles out day in and day out. This is NOT about Trump who you appear to obsess about but about ‘Election Integrity and Transparency’. Without this there is no such thing as ‘Democracy’. It really is that simple Justine and you really need to take a breath with your ‘Holier than Thou’ attitude. Agree to disagree about anything or any subject as that is your opinion but please show some courtesy and a little respect when on a public forum.
Sounds like your confidence in the results are high? If so do you agree a full forensic audit of those 6 states should be completed to heal our nation?
If Biden won the popular vote overall, what does It matter .. to democracy?
He (It because he is only a puppet or Trojan Horse) did not “win” any popular vote….
Watch and see…..
Ha yeah that person clearly didn’t even read all of this info to say Biden won pop vote lol
Patrick you keep referring to an investigation into the security of the 2018 Dallas election but I can’t find any reference to that. It would seem a public expenditure of that size would generate some record at the very least of it having happened.
Where is that documented? Will you ever share the findings?
Thank you. I am not speechless re the oppositional party who seeks to destroy America. I respect you as I respected my Dad, the late CDR TA DeRobbio, who fought without a thought of what he left behind. You are good.
This would make an interesting graph.
https://humansarefree.com/2020/12/chinese-royalty-counterfeit-ballots-printed-in-china-shares-phone-call-and-pictures.html
Do you know where I can find a tv replay of election night results that so minute by minute election vote totals for Presidential Election?
Great work Patrick. Keep it up. The Country is behind you.
Check this out:
https://youtu.be/UgeqGmvQXKs
Can you update on the safety of Pres Trump?
Lol- you the man !!! Format was off I found it.
STAY HOME AND STARTING WORK AT HOME EASILY…Make 6,000 dollar to 8,000 dollar A Month Online With No Prior Experience Or Skills Required. Be Your Own Boss And Choose Your Own Work Hours.
Thanks A lot Here………. http://www.Jobs82.Com
Does Sidney have access to your graphs?
A week ago. I wanted to let her make them up unlucky first but with violence in the air…. I’m taking unilateral action.
STAY HOME AND STARTING WORK AT HOME EASILY…Make 6,000 dollar to 8,000 dollar A Month Online With No Prior Experience Or Skills Required. Be Your Own Boss And Choose Your Own Work Hours.
Thanks A lot Here………. http://www.Jobs82.Com
So you’re saying that you’re too dumb for what appears to be the world’s dumbest lawyer to take seriously?
STAY HOME AND STARTING WORK AT HOME EASILY…Make 6,000 dollar to 8,000 dollar A Month Online With No Haz Prior Experience Or Skills Required. Be Your Own Boss And Choose Your Own Work Hours.
Thanks A lot Here………. http://www.Jobs82.Com
I deeply thank you, Sir,
I thank you so much for your efforts and for putting this together. I sincerely commend you,
We went to Washington DC last weekend for the March to support our President Donald Trump. I truly believe that Donald Trump IS the winner of the 2020 election. The absence of the democratic party in our media since the election is not even believable. The aspect of what cheating went on in specific states was a TARGETED effort to skew the election for dimwitted Hiden Biden. Even though the daily news cites that everything is over, which I refuse to follow for many reasons. The crowd in DC was between 500,000 to 750,000 people if not more. I know I was there. Also, we went to the Lincoln Memorial on Sunday. Where a Trump supporter with a Trump Flag stood in front of the Lincoln Statue and waved that flag to which we all chanted how proud we are of the USA. About 30 or so of us present at the time. We have a video of this. We were almost immediately shut down by the DC park police, under the threat of giving us all tickets for unlawful assembly.
I love this country and am sick and tired of the corruption at the highest levels of government and want to start seeing people that have broken election laws go to jail.
Regards,
A. Wegener
I was there as well A. W. Thanks for coming. There were a lot of people at that event, I will attest to that.
Thanks Patrick for providing this info for the doubters. I truly think most of us believe this election was rigged. Whether D or R, the whole thing just fails the logic test. You are a true Patriot Sir and I thank you
Thanks for all your work on this fraudulent election, Patrick! I really appreciate it, and I think you are dead over the target with your analysis. The one thing I and many others have been concerned with is how do you explain the computer data theory to a computer illiterate court, and I think I have come up with a simple solution.
Basically, Trump’s lawyers need to simulate the voting system and demonstrate how the “flip” or vote transfers are done. And to do that they need to setup a couple of Dominion voting machines; a server to capture the votes; someone on a server-attached computer with the software used to control the vote; and people to vote a certain way. Once they vote, the computer operator could demonstrate how the votes are transferred or flipped to the other candidate. And even with that they may be asked if they have proof it was done. Of course, Trump’s lawyers would have the charts showing the spikes, but they will possibly need people to testify that they did it, or they coordinated or watched someone do it. Hopefully other data showing how poor of a candidate Biden was will lead the court to decide the election was stolen.
I’m praying for Sidney Powell, and that reminds me. I need to send her a donation.
Thanks Again For Your Great Efforts!!!
here evidence
Scroll down they are there!
This is actually conspiracy theory stuff. He does not actually prove anything.
Conspiracy blah blah blah, conspiracy blah blah….. My brain got stuck.
Your sure didn’t KARERN !
Your mouth sure didn’t just another Carrion eater.
Conspiracy theory is just a term used by those too lazy to do their own research.
hello
hello
hy
STAY HOME AND STARTING WORK AT HOME EASILY…Make 6,000 dollar to 8,000 dollar A Month Online With No Prior Experience Or Skills Required. Be Your Own Boss And Choose Your Own Work Hours.
Thanks A lot Here………. http://www.Jobs82.Com
Thank you, thank you, thank you.
Please keep up the good work and know you have thankful supporters.
so how can we stop this. everyone knows he cheated.everyone.but they have mainstream media and everyone else on there side
Patrick and all, there is evidence that dominion voting machines can be traced to London and that Venezuela is true but just not the source
75 million Voters who voted for
President Trump have been duped!
Thanks for all the info Pat, good stuff,, i also heard the DID got dominion servers protected by the CIODin germany,, keep up the good work!!
Michael this WAS a conspiracy. You’ve been so fooled by mainstream media that you now MISUSE the word! Many people CONSPIRED here in a clandestine manner to do something nefarious. THAT my friend is the DEFINITION of a CONSPIRACY. Dictionaries are helpful brother!
: )
Thank you, Patrick. I am hoping more people like you can save the Republic, but despite all the evidences, the psyop prevailed. We cannot be ruled based on fraud and false flags but the perpetrators don’t get punished. I am heartbroken because the infiltration of evil and corruption are all over the place. I thought the truth will set us free, but it is not enough if evil is not punished and rooted out. Please do what you can and all the white hats for President Trump and his family. He gave his best unselfishly. I hope for a happy ending.
What browser are you using? I only use the DuckDuckGo browser app.
Thanks for working on this, Patrick.
My honor
Thank you for your fine work so many of us feel the vote was our last form of power in choosing the direction we want our great country to go but now that has been stolen from us!
hlo
THANK YOU Patrick!!! God bless & protect you my new patriot friend!
Have you ever investigated Fraction Magic? Bev Harris is first one I heard of it from. Here is a search result on the DuckDuckGo search site. NewsWithViews also has Devvy Kidd, another long time vote fraud investigator.
https://duckduckgo.com/?q=fraction+magic+bev+harris&t=h_&ia=web
Many Thanks to you Sir!!
SamFox
https://duckduckgo.com/?q=fraction+magic+bev+harris&t=h_&ia=web
Here is a message I sent to everyone on my email list.
New Vote Fraud Expose’.
Saw this at either NewsMax or OneAmericaNewsNetwork. These are two news channels that are very good. They also have websites.
https://www.deepcapture.com/2020/11/election-2020-was-rigged-the-evidence/
If you have not heard of these, look up War Room, a web news site and UtahGunExchange.com, a new alternative to YouTube. You have probably heard of Parler, an alternative to Twitter.
I do not mean to over burden anyone, but the USA is in the midst of a New World Order attempt at a takeover of the USA as we were founded. That is what’s behind the riotous ‘peaceful protests’, leftist media propaganda, the new Dem left platform & the current election battle for Congress & White House. One term for this mess is Color Revolution.
https://www.conservativedailynews.com/2020/09/what-is-a-color-revolution/
https://thedailycoin.org/2020/08/11/the-george-soros-color-revolution-in-america-is-in-progress/
God bless the USA and all of you!
SamFox
Again, Patrick, MANY MANY thanks!!
This is an message I sent to everyone on my email list:
New Evidence Of Election Fraud;
Saw this at either NewsMax or OneAmericaNewsNetwork. These are two news channels that are very good. They also have websites.
https://www.deepcapture.com/2020/11/election-2020-was-rigged-the-evidence/
If you have not heard of these, look up War Room, a web news site and UtahGunExchange.com, a new alternative to YouTube. You have probably heard of Parler, an alternative to Twitter.
I do not mean to over burden anyone, but the USA is in the midst of a New World Order attempt at a takeover of the USA as we were founded. That is what’s behind the riotous ‘peaceful protests’, leftist media propaganda, the new Dem left platform & the current election battle for Congress & White House. One term for this mess is Color Revolution.
https://www.conservativedailynews.com/2020/09/what-is-a-color-revolution/
https://thedailycoin.org/2020/08/11/the-george-soros-color-revolution-in-america-is-in-progress/
God bless the USA and all of you! (End of sent message)
SamFox
You deserve the “ Medal of Honor” for exposing the “demon-rats“ crimes.
Don’t give up !
Eric Glanzer M.D. & Nancy Ganzer
Colorado
I’d settle for a pardon. 🤣😂🤣😂😅
Don’t you have a get out of jail free letter?
“ Medal of Freedom”
Thank you for trying to get to the bottom of this rigged election. I hope you have made this information available to Sidney Powell, Lin Wood, Hordan Skeulow, Jenna Ellis and Rudy. If Biden does become president, he will be out almost immediately. Both Kamala and Biden have said, “it’s the Harris Administration w/ Joe Biden.” If Democrats take over the White House, senate and house by cheating, our country is screwed, I hope you love our country enough to jump in and help Trumps campaign prove this fraud in court. We need more good men like you! please don’t let democrats have this election by getting away with a rigged election. Look at the cabinet Biden’s putting together. Our country will never recover from the damage they will do! Thank you again, Be safe. Be well. God Bless. Darlene
Patrick,
You truly are an American hero. I sincerely mean that. I homeschool my daughter and after the election fraud evidence started coming in, honestly I just stopped teaching her the Constitution,-what’s the point?it seems futile. You give me hope that’s not the case. I want to be able to tell her we have a free republic. Thank you.
Thank you Patrick.
First saw you with BCP.
https://drrichswier.com/2020/11/23/nevada-washoe-county-clark-county-are-counting-duplicate-voters-contested-ballots-unregistered-voters/
More numbers for you to run
Ok….I have read the entire back story and I
belief everything…..Love the Taxi skit to describe the situation…They say fact is stranger than fiction ….I used to think The most Interesting Guy in the World was an advertising campaign….but it must have been based on You . You are up there with Paul Revere ….you should get the Freedom Medal…..no one should have to pardon you for being a Patriot….a courageous example…of Country above self.
Duty …..Honor ….Country…proud to be an American knowing people like you still exist…Bridges of Tokyo Ri…..last line in the movie…..Where do we find such men?
.
https://www.youtube.com/watch?v=Hl30AijmQvI
Philipines TV interview 2015, Mark Malloch-Brown admits license agreement bet. Smartmatic & Dominion
{“trumpd”:0.566,”bidenj”:0.42},”votes”:2984468,”eevp”:42,”eevp_source”:”edison”,”timestamp”:”2020-11-04T04:07:43Z”},{“vote_shares”:
{“trumpd”:0.56,”bidenj”:0.426},”votes”:2984522,”eevp”:42,”eevp_source”:”edison”,”timestamp”:”2020-11-04T04:08:51Z”},{“vote_shares”:
Interesting. Between 4:07:43 and 4:08:51, Trump lost (approximately) 17,876 votes and Biden gained (approximately) 17,929 votes.
I gather it came from here:
https://static01.nyt.com/elections-assets/2020/data/api/2020-11-03/race-page/pennsylvania/president.json
Is there an index of this kind of data? An explanation of where it comes from?
Upon closer examination, both candidates appeared to lose votes at various times. I think that urges the question: what does this data actually mean? Where does it come from. Inquiring minds want to know.
I read yesterday that you are the number one threat to the deep state. WELL DONE, SIR!
You sir are a true patriot. Let justice be done though the heavens may fall!
Inshallah.
B’ezrat HaShem (Hebrew replacement for your Arabic expression…) ” With God’s help!
From your lips to G_d’s ear.
Thank you !!!!!
Patrick where did you get the 1.4 million mail in ballots sent back and 1.8 mil requested. I see some places say 3,030,000 requested mail in ballots.
Give link please. But those numbers were taken from a snapshot of the PA election’s office website on the afternoon that I published them. They had shown those numnbers all day. After I published they took some of the numbers down entirely. They may have put fixed ones up since then.
@PatrickByrne:
The fact that PA hid that mail ballot dataset is practically criminal.
Do you have a screenshot showing the number of general election ballots issued or returned (not primary)?
A screenshot was taken, I am told. Checking into it. Will post that.
Now there is a version with the data hidden.
Where you allowed to see the actual scanned ballots being run through the dominion machine? Or ascertained by the counting? Here’s the big question if a reasonable judge looked at this hard evidence would he/she come to the give President Donald Trump 4 more years or would they cow down to the mob?
Occasionally, just now and then, could you use the Hebrew instead: B’Ezrat HaShem!
THANK YOU Patrick!!!! God bless you for your honest work! I am ngoing to send your site to everyone I know!
Have you ever investigated Fraction Magic? Bev Harris is the 1st one I know of to expose it.
https://duckduckgo.com/?q=fraction+magic+bev+harris&t=h_&ia=web
Thank you for your services Patrick I listened to you last night on Pete Santilli show. Not being business oriented or overtly political I had never heard of you I am now starting to realise that I need to be much more involved. Thank you for coming on the show and giving us much needed info. God bless you and yours
Thank you Patrick. I’ve followed you since 2013 as a precious metals & crypto enthusiast. In addition to the dominion fraud, I have done citizen audits in Absentee voter registration lists in Wisconsin, and personally witnessed hundreds of fraudulent & Literal duplicate votes which are unquestionable as the public data can be accessed by anyone. The fraud takes place by people voting under multiple assumed identities. I.e someone who goes by Christopher as well as Christine.
This is a multi pronged attack using ballot harvesting, fake / duplicate votes, as well as the malicious cyber activity you outlined.
Thank you for your commitment to the truth.
Thank you for all you and your team are doing to get the truth out!!
THIS ELECTION IS A FRAUD CAUSED BY THE LIBERAL MACHINE
In my opinion..
I guess you have not hear that this also involves John McCain in the past and also Mitt Romney past and present. This is not partisan this is corruption and it is on both sides of the isle.
BTW, we use the word “liberal” around here in the classical definition. Many of use are Libertarians.
I get paid more than $120 to $130 per hour for working online. I heard about this job 3 months ago and after joining this i have earned easily $15k from this without having online working skills. This is what I do…..___bit.ly/GoogleJobs16
Can you please stop posting your work at home stuff? It is a real distraction. Thanks.
So weird how a tech genius like Patrick can’t figure out how to moderate the comment system on his website…
nice to see- open eyes to all sorts of hacking….
not just voting machines….
and thank you A DAMN GOOD one man show.
every honest person wants the truth regardless of party.
Keep up the good work!
keep at finding the truth!!
retired USMC…”against all enemies, foreign and domestic”
That’s what I always say.
I think we need to come out of retirement and fix stuff. Remind cops, judges, politicians we all swore an oath.
“Lock it up!”
That’s what I always say.
I think we need to come out of retirement and fix stuff. Remind cops, judges, politicians we all swore an oath.
“Lock it up!”
Will you be able to present your findings to the Supreme Court as evidence of systematic election corruption?
Thank you for exposing the darkness. We are all in your debt.
Proof Scytl had servers in Germany and how they tried to hide it.
https://rumble.com/vb718d-scytl-and-dominion-are-lying-to-you.html
what is the time zone difference from their server location moves?
Great work!!! The problem is that we need to make this so loud that they cannot ignore it. Trump should hold a press conference and put this out there. Then he should call out DOJ, Barr, Durham, FBI, Wray. These guys are commiting treason by just standing by.
How can I subscribe
In Georgia and Pennsylvania the strategy seems to have been a long and statistically impossible series of 4800 (Georgia) and 6000 (Pennsylvania) vote dumps beginning after 10 PM on election night. see centralcitynews.us
This is just a rounding issue. The underlying data reports the vote total, and then the percentage of those votes going to each candidate. These percentages are only given at .1% precision, so the smallest change in a candidate’s vote total that can be detected is .1% of the overall vote.
You can check that the “vote dumps” are almost exactly .1% of the vote total, which is why you see about 4800 in Georgia (about 4,800,000 total votes) and 6000 in Pennsylvania (about 6,000,000 total votes).
Yes, you are right. But what about the spikes?
It’s again just a rounding issue. At a precision of .1%, you’re not going to detect relative changes in a candidate’s votes smaller than .1% of the vote total. I’ll illustrate with an example. Suppose you have the following sequence of updates:
Biden Trump Vote Total
49.4% 49.3% 6670421
49.4% 49.3% 6670727
49.4% 49.3% 6673676
49.4% 49.3% 6673812
49.4% 49.3% 6673827
49.4% 49.3% 6673851
49.4% 49.3% 6673915
49.4% 49.3% 6678806
49.4% 49.3% 6679106
49.4% 49.3% 6681723
49.5% 49.3% 6688707
The candidate percentages remain unchanged until the last update, where Biden’s percentage changes by the smallest possible amount. Now, let’s suppose for the sake of argument that on the first row Joe Biden has exactly 49.4% of the total vote, and Trump has exactly 49.3% of the total vote. Or, at least, as close as they could possibly be to exactly those percentages. Their votes would be:
Biden: 3295188
Trump: 3288518
Now, that first update adds 306 to the total number of votes. If all 306 went to Biden, his percentage would increase from 49.4% to 49.402% (rounded to the 1000th place), while Trump’s would decrease from 49.3% to 49.298%. Rounded to the nearest .1%, both Trump’s and Biden’s percentages would remain unchanged. Same idea if all 306 went to Trump. So, how did those 306 votes get distributed between the two candidates? The answer is, we don’t know, and can’t know given the precision of these numbers. It’s a mistake to conclude because the percentages stayed at 49.4% and 49.3% respectively that the 306 votes split equally between Biden and Trump. And this isn’t even taking into account that some of those votes are probably for other candidates, which adds a little more uncertainty.
So, what can we know? If you take those 10 updates in aggregate, that Biden comes out around .1% of the total (6700 votes) ahead of Trump, but we definitely do not know that all those excess votes came as a spike on that final update. All the analysis I’ve seen around this particular claim is based upon this misunderstanding.
Hope that’s clear.
Hope this is clearer Dylan: Drop and Roll: How the Dems Tried to Steal the 2020 Election
I will be adducing this data into the article as well.
I think the election was stolen, seems as obvious as it could be. But I have looked at data every day for 20 years – I am worried there are rounding errors here also, that will water down what would otherwise be a solid case.
Patrick, maybe you could explicitly tackle this in your analysis?
And yet by your own admission the vote count is manipulated. And a whole lot more than you claim. My question for you is this Dylan. Why are you OK with any voting manipulation?
A vote, is a vote, is a vote. Once counted it does not change, and yet we have this here in every swing state. Why are you trying to justify the stealing of an election? Why are you trying to say since it is so little it doesn’t matter? You are disengenuous at best.
The 100k mysterious Michigan votes were ruled out as a clerical error that was detected within 20 minutes. Some stories never die.
This is in response to two comments. It appears I can’t reply after a certain depth, but I’ll specify as best I can to whom I’m responding.
Patrick – You’ve probably moved on to other things, but I did take a look at that “Drop and Roll” video you recommended. The analysis is entirely based upon a failure to understand elementary school lever rounding. I can provide more details if desired, but the only thing it proves is that whoever put together the analysis has no idea what they’re doing.
Anonymous – Or, whichever one of the many anonymous posters accused me of being OK with voting manipulation. I’m not, and never claimed to be. I’m not saying that it’s so little that it doesn’t matter. I’m saying that, as with the Gateway Pundit video Patrick recommended, the issue is that the person doing the analysis doesn’t understand how to deal with a rounded value, and with that understanding the particular claim of voter fraud goes away. It’s not that it’s small, it’s that it isn’t there.
I can provide explicit explanation with details if desired.
Realized my first explanation might have been a bit too involved. Here’s a more simple example. Suppose you have 9 updates, and at each update Biden’s percentage of the overall vote changes by .01%. The rounding to the nearest tenth of a percent is also provided:
48.66% -> 48.7%
48.67% -> 48.7%
48.68% -> 48.7%
48.69% -> 48.7%
48.70% -> 48.7%
48.71% -> 48.7%
48.72% -> 48.7%
48.73% -> 48.7%
48.74% -> 48.7%
48.75% -> 48.8%
If you’ve only got precision to .1%, it will look flat until you finally see that .1% “spike” at the end, even though the underlying changes are much smoother than that.
Hi Dylan, then why is the spike in Michigan ~100k? Does that mean the total votes in Michigan is 10^8?
you’re showing a fraction of a percent rounding issue. We’re seeing a 15% jump in some states
Hi Dylan, then why is the spike in Michigan ~100k? Does that mean the total votes in Michigan is 10^8?
Hi Dylan, then why is the spike in Michigan ~100k? Does that mean the total votes in Michigan is 1e8?
It seems I can’t reply directly after a certain depth, so this is in response to the questions about those other spikes.
My response doesn’t address those. It’s specifically in response to the question about the sequences of approximately 4800 (Georgia) or 6000 (Pennsylvania) votes, which I thought were the spikes to which the questioner was referring.
But no, the spike in Michigan is definitely not a rounding issue.
True American hero, thank you (and the team) for your service!
Thank you for everything you’re doing! I’m sharing this information as much as possible!! I know the heat is on the Dems because Biden tweeted “This election is over” this morning. It’s not over!!!
“We the People of the United States, in Order to form a more perfect Union, establish Justice, insure domestic Tranquility, provide for the common defence, promote the general Welfare, and secure the Blessings of Liberty to ourselves and our Posterity, do ordain and establish this Constitution for the United States of America.”
Thank you!
Just watch interview on OAN ! Kudos to you !
💯 % support your work!
Thank you , may God bless your work!
Me too…
I’m a fan but think you are misguided on the AZ sharpie gate. I was a poll worker. First you need to address Maricopa’s official statement. https://youtu.be/aNhCcimt6No On Election Day mostly sharpies were used and virtually all were read by the tabulator. Yes there were overvotes but the tabulator identified the race and most were on judges – we had many of them. I’m not saying that they didn’t have a nefarious reason for requiring sharpies but I don’t think is was to kick out ballots (maybe it was easier to allow these votes to be switched?) Please address this because, IMO, your position on the AZ sharpies demeans your entire thesis.
Of course, this is from “Karen”
Says the guy that is so such of himself that he pipes in as “Anonymous.” Grow up!
Karen has made a good contribution from eyewitness experience and is trying to make the case more persuasive.
to the commenter : knock off the Karen stuff. the intent of the Karen meme is to intimidate women from being part of the conversation
Thanks Jay. That was exactly my point. I saw thousands of these ballots being fed through the tabulator. None of them showed an “over vote” for the presidential race (prior to “pressing the green button” there is a small LCD screen that described what race causing the problem – and most were in judge races). Also, they all went through as being counted. With all due respect, I’m not sure Patrick has actually seen how the tabulator worked. His explanation of how the tabulators worked is generally correct but is missing specific details. Based on how he has described it, the “pool of ballots” that they could play with would be the ones that couldn’t be accepted by the tabulator (and were put in the front slot). Out of the 1k+ ballots at our site there were probably only 20 or so ballots that went into this slot. Also, at the beginning of day a tape was printed that showed zero votes for each race. At the end of the night a tape was printed that showed the number of votes for each candidate in each race (it was a very long tape). If there was any “vote switching” going on, my opinion – as a CPA and former auditor who worked at one of the largest independent accounting firms – it could be pretty easily detected by a hand count of the paper ballots compared to this tape. Just saying. We need to make sure we are dealing with facts.
Where you voted, was everybody told they needed to use Sharpies? If they had been, perhaps you would have seen more than 20 votes to adjudicate.
It wasn’t where I voted – I actually worked at the site on election day from 6 am to 8 pm. And yes, everyone was using Sharpies – that is what we were handing out. If anyone asked I explained it was due to the time needed for the ink to dry and wet ink causing issues with the tabulator. If anyone insisted, however, on using a ballpoint pen (mostly because they didn’t like the bleeding) they were allowed to use the ballpoint pen. I would say that 95% of the ballots at my site – on election day – were filed out with a Sharpie. And no, there were no more that 20 votes that needed to be adjudicated. The large majority of the “sharpie” ballots were fed into the tabulator and the message on the LCD screen indicated that they had been accepted. When there was a problem it usually related to a judge race (and once we kicked the ballot out to review it, I could see why it was rejected. Typically, the voter had completely filed in the “yes” oval but had a small mark in the “no” oval. I told them they could go get another ballot and start over. Or, they could completely fill in both the “yes” and “no” ovals for that race – most choose this option. Once they did that, when the ballot was fed back in, the LCD would show an over vote for that race and then the green button would be lit. If they pressed that button, the ballot would be accepted. I understood from my training by Maricopa, that by pressing that button they only race that wouldn’t be counted would be the one with the over vote. NEVER did I see an over vote for the presidential race.
I saw a video that demonstrated that when a Sharpie is used, the ballot doesn’t work. The person Sharpied a ballot, the ballot wasn’t read. Then the ballot was taken to a screen that could vote for anyone the person handling the ballot wanted to click in. It was a way of changing who was 1st voted or making sure the ballot handler’s choice was put in. .
I also understand Sharpies were used in R heavy districts.
SamFox
I’m not sure a video from the very people who may be committing a crime is the correct one to use to back up your opinion. If you ask a criminal if they committed a crime, they will tell you no. Are you supposed to ignore the mountain of evidence against them? This also doesn’t explain why poll workers told people NOT to use their own ballpoint pens, and “only” use the sharpie pens. Nor does it explain why poll workers were telling people to ignore the “warning” sign popping up on the machines after people fed in their ballots and to just hit the “green” button anyway to submit the ballot. People who did this were later seeing their votes not recorded.
Shawn, I agree. But. In order to defend your position you need to refute that opposing view. Maricopa’s explanation for the using sharpies on election day and ballpoint pens for early voting was due to the time it takes for ink to dry on sharpies vs pens. They said that the wet ink caused malfunctions in the tabulator. Sounds like that can be something that should be easily verified. So, to answer your question, that’s why they told people not to use the ballpoint pens (although if someone used a pen they were accepted and fed through the tabulators). As for the “warning” signs, with all due respect, I don’t think Patrick has described it as it actually happened. Has he seen one of these machines in action? I have. What happened is that once you fed the ballot through one of two things would happen. Option 1: The ballot would be accepted (dropped into the box underneath the tabulator) and the LCD screen would show a large green check mark. Option 2: The screen would show a message saying there was a problem (identifying which race). The ballot would still be in the tabulator. There was a green button (accept) and a red button (return ballot). Most of the times, when there was a problem only the red button would be lit – meaning that the workers wouldn’t have been able to tell the voter to “just hit the green button. They would need to hit the red button, the ballot would spit back out of the machine and the voter could then correct the race that was indicated as the problem. After feeding it back, if there was still a problem (which would be described on the LCD screen), they were then given the option of hitting either the green or red button. My understanding is that by hitting the green button, it was only affecting the “problem” race – which – as I said – was usually a judge race. Never did I see an over vote on the presidential race. As for “people seeing their votes not recorded” there is no way that relates to the election day votes. IMO, that occurred when a voter had been mailed an early ballot and choose instead to vote on election day. The “not recorded” or “cancelled” message that they got if they checked their vote on the Maricopa website was in regard to the early vote being cancelled since they logged in on the site book on election day to vote in person. Again, I am not saying there wasn’t something in the software that was playing around with the votes but what Patrick is describing doesn’t jive with my personal hands on experience.
Sharpies were used and when scanned the tolerance of the machine could be adjusted to require adjudication. The adjudication could then be overridden and the person doing the work select any candidate they want the votes to be given to. Having REP vote in Sharpie made it easy to consolidate the Trump votes, have issues with adjudication then flip all those to Biden with override.
Perhaps. But as I said, once the ballot was fed in the LCD screen would indicate successful tabulation with a green check mark. I don’t see how this would allow for later adjudication. Also, to be clear, EVERYONE was given Sharpies on election day – not just republicans. Based on the voter registration cards and the electron site book used to check the voters in, I would say that our voters were pretty evenly split between reps, dems and independents. Finally, they would need to contend with the actual paper ballots and end of the night tabulator tape showing the vote counts. If votes got switched, it would be detected by an audit of the paper ballots vs tape vs official count. While Maricopa has not done a full audit, I understand that they did audit 10% of the voting sites.
i dont really understand everything about how the proces works but i think the only goal of the dnc is the get rid of trump and the long game they have is that pelosi becomes acting president and trump gets indicted because he loses immunity after jan 20 and then he cant become president anymore. biden is just a puppet in this story
This is interesting but entirely lacking in “evidence”. The Wall Street themed articles are almost nothing but evidence. When does that change?
What do you mean by “The Wall Street themed articles”?
More importantly, what does he mean by “evidence”?
Evidence. You know, facts.
If you have “thousands of affidavits” why not post them? Also care to elaborate on why Powell was publicly disavowed by the Trump team but you claim she has the evidence?
It almost feels bad to beat down these ignorant fools with math and forensics.
This site used to be focused on proving stock market fraud. Patrick, when you used to say “Herb Greenberg and Camelback Research work together to manipulate stocks” you would show us the emails proving it. Or trading data. Or affidavits. Or whatever.
That’s evidence.
“Smartmatic election software was developed in Venezuela” is not evidence. Why not link to non-Qanon sources? Or any sources?
“Dominion’s servers are widely infected with QSnatch malware” is not evidence. Why not provide some? I can’t imagine you figured this out on your own.
“ballot processing velocities physically impossible given available site equipment” you may be right but how do you know? What are reasonable processing velocities? What was observed?
The old Deep Capture would have provided all this.
Well I am rushing to get a lot of stuff up so that people do not wait any longer. I have just spent an hour expanding this with more material and more links. Keep checking back. I left a footnote that said that I am doing so.
With the votes being easily changed in each machine isn’t likely that there is vote changing going on all over the country on smaller levels. I find it hard to believe that the portland mayor got re-elected legitimately and also some of these idiots in the squad
Your information is totally wrong. The basic premise of your argument is wrong and debunked. Smartmatic and Dominion are not tied in any way. Please see link: https://www.reuters.com/article/uk-factcheck-dominion/fact-check-dominion-is-not-linked-to-smartmatic-antifa-or-venezuela-did-not-switch-u-s-2020-election-votes-in-virginia-and-was-not-subject-to-a-u-s-army-raid-in-germany-idUSKBN2861TB
Your data is doing more damage to the country than it’s helping anything. Do some research before spouting off thinking you have actual evidence. Also, if you’re going to post charts showing that Biden votes were injected, you need to absolutely link that data in so that someone else can analyze it, otherwise it reeks of fraudulent claims.
Deadheded Says:
November 24, 2020 at 8:53 am
https://www.youtube.com/watch?v=Hl30AijmQvI
Philipines TV interview 2015, Mark Malloch-Brown admits license agreement bet. Smartmatic & Dominion
So the Chairman of the Board is lying about licensing smartmatic software?
the 4X capacity speed on the ballot counting machines was done by a cyber systems expert from dallas texas who survey the systems and gave a affidavit already on this event that puts those large vote spikes in question. How did they get into the voting system in that time period a lot of people are now asking?
I completely agree. How would he know as to what malware, if any, existed on a Dominion voting machine? Do Dominion Voting machines even run on QNAP… which is what QSnatch targets/runs on? I saw this posted by some weird guy on Twitter (https://twitter.com/We_Have_Risen/status/1326697422362435585) that just kept posting random screenshots with leading questions without having any idea what he’s talking about.
QSnatch can infect much more than just QNAP NAS applicances which actually use an embedded Linux operating system. It can infect Windows too. It could infect Linux servers hosted in the Cloud. It can install itself into browsers, etc. It’s particularly nasty piece of malware whose operators are rather sophisticated. The thing about malware is that it evolves. Pieces of one malware become added to new malware. Dominion software is so incredibly bad about security it wouldn’t surprise me at all to hear their servers have malware. Doesn’t matter if it’s QSnatch or any other malware. Their entire architecture and design is severely flawed. But even with the absolute best security and best design practices all digital systems are subject to fraud and abuse. People buying those smart door locks where hackers with an Android phone can unlock them with ease. Telsa keyfobs and mobile apps have a flaw that allows anyone with the knowledge to drive off in any Tesla in mere seconds. Perhaps easier and faster than trying to force a mechanical locking mechanism.
Elections with a ballot paper trail and hand counting is slow and tedious but the results can be observed, monitored and verified accurate. If these digital solutions were so much better then why are they still counting? It’s been 17 days! Come On Man!
That guy on Twitter seems to be posting screenshots of bitwise Assembly language, which is what one can observe when a compiled application runs in RAM. And it can tell you next to nothing about what’s going on…only how values are moved around in memory. But it sure looks complicated and intimidating.
Curious what a sharpie/bic switcharoo is? I don’t watch the news so I apologize if this is already well-established knowledge.
In Maricopa County (Arizona) voters reported that the precincts made them use Sharpie pens to fill out ballots instead of bic/pens. This was to take advantage of a feature in the voting system called an adjudication queue. Sharpies bleed through the paper which causes the voting machine to fail to register the vote. It falls into a special queue that allows the poll worker to manually view the ballot image and drag and drop the vote into the appropriate candidates bucket. The problem is the feature allows you to drag and drop hundreds of items from the queue at a time so, an enterprising fraudster can fool voters into using sharpies to force their ballots into the special queue and then voila, they can just assign the votes to whomever they want to.
As I’ve described above, I was a poll worker in Maricopa (and have been on the Trump train since day one). Patrick’s explanation of the “adjudication queue” is inconsistent with my first-hand experience. Virtually all of the election day ballots at my site were filled out with Sharpies and most of these were registered by the tabulator as being counted. That is not to say that something happened later in the tabulation process but there was not a mass rejection of the Sharpie ballots. And, everyone – not just republicans – were given Sharpies on election day.
Straw man argument. Nowhere did I claim that in Maricopa only Republicans were given Sharpies. You just made up that claim and put it on me.
Patrick, I’m on your side. I’m not trying to put anything on anyone. I know that there was fraud in this election and I want to get to the truth. I clarified that ALL were given sharpies – not because you said it (you didn’t) but because some of the other comments seem to be under the impression that Sharpies were given out strategically. It doesn’t help us if we go down the wrong rabbit hole – a hole that the dems might have put there to distract us.
In most parts of the county, voters on Election Day were predominantly Trump supporters. So Trump votes could be more likely affected if the change to sharpies occurred on election day.
There was a letter sent out by an election official instructing precincts to use ballpoint pens for the days leading up to election day, but to switch to markers on election day. Exact quote: “We NEED to use Markers on Election Day, but for now and through 11/2, hand voters a Ballpoint Pen. You have plenty of pens in your supplies right now.”
NEED?
That sounds very suspect. You can read the letter here. https://nationalfile.com/leak-email-allegedly-from-maricopa-elections-office-found-issue-with-sharpies-said-use-them-on-election-day-anyway/. This election official has now deleted all of her social media.
Furthermore, Arizona instructions for filling out ballots recommend you don’t use a Sharpie. Here: https://www.thegatewaypundit.com/2020/11/arizona-ballot-instructions-specify-not-use-sharpie-may-not-read-tabulator/
I don’t know what shenanigans were going on, but it’s likely a poll worker (like you) wouldn’t be told the reasons behind the switch from ballpoint to Sharpie on election day. Her email tips her hand. I remain unconvinced that nothing nefarious was afoot.
Thanks man. I love it when readers do some of the work for me.
From the lead article–
“[v] By way of example: Sharpie/Bic switcheroos experienced in Maricopa precincts reflect a wish to generate a large pool of “adjudicated ballots” for administrators, who could drag-and-drop them later to Candidate Biden.”
I saw a demonstration video of that happening where such a Sharpie Switch was proven possible.
SamFox
I want to bring up something I have heard NOTHING about in Arizona. So my son’s father who a long time ago put his drivers license address to my home…. he has never registered to vote. This election I start getting voting stuff at my address for him. Then my friend Andy at his drivers license address which remains his mom’s address, gets a ballot… he also never registered to vote. In Arizona, to register or check your registration status you need a few personal identifiers… and an identifier of choice such as last 4 of SS#, voter ID# or “Drivers License” number…. so it seems someone with access to DMV records was registering unregistered adults using the driver’s license info. Andy never registered himself because he is a felon and has not gone through the process to restore his rights… but Arizona seems to be in an on your honor system with felons and voting… as the Maricopa County recorder says his voting status is “active”. One he never registered for!
Thank you , God bless you always! The truth always prevails.🇺🇸🇺🇸🇺🇸🇺🇸😎👍
Keep giving us the information Patrick and we will spread it. Thank you. You are a patriot.
Thank you Patrick and God Bless You for the work you’re doing!!!
Patrick, thank you so much for this. Do we have evidence of who ordered and directed this fraud?
Yes
Will the true evil-doer be exposed by you or Sidney soon?
Oh, my!!!! I’m excited/nervous. I hope we can preserve America. I’ve been telling my 11-year-old son that I don’t know what the heck is going on, but that this isn’t the country into which I brought him or in which I was raised.
GLAD YOU FOUND THEM OUT >> I THOUGHT THEY WERE STICKING SOMETHING ON THE MACHINES TO CHANGE THE VOTES UN THE DARK >> WONDERED IF THEY HAD CAMERA S ON THESE MACHINES << NEVER SEEN THEM CLOSE A ELECTION PLAC IN MIDDLE OF COUNTING ITS UN HEARD OF IN THIS COUNTRY << HOPE WE GET TO THE BOTTOM OF THIS RACKET
If it can’t be “unscrambled” does this mean they get away with the fraud?
Clearly you aren’t taking your meds anymore.
Hard to argue with logic like that.
PB. I have been looking over the election json file feeds from Edison. Like this: https://static01.nyt.com/elections-assets/2020/data/api/2020-11-03/race-page/pennsylvania/president.json
What I don’t know is how this information is gathered and interred into the tally. Is there a human somewhere in the mix or are these taken from a direct feed from the counting “machines”. In other words I don’t know the integrity of the data. Could the vote switching I see be human error or is this “valid” data and these inconsistencies are some of the evidence? If this is good data then the vote switching is simple enough to see that I can explain it to my family over the holiday week…
Any insight on this or other public sources of data you can point us too would be helpful..
I voted but not for any of the old white guys with valid rape charges against them.
Dear Mr.Byrne ,
as a UK citizen I would just like to say a deep thank you for your decency and hard work in protecting democracy.
So many dead on Normandy beaches. We must all never forget and must fight this very obvious coup.
P.S. massive CNN propaganda over here ( equivalent to Nazi artillery shelling of Omaha Beach in a desperate attempt to prevent the truth getting a foothold).
God Bless America and its constitution.
Spent two of the best years of my life up at Cambridge, courtesy of Her Majesty (as a Marshall Scholar).
PB. I have been looking over the election json file feeds from Edison. Like this: https://static01.nyt.com/elections-assets/2020/data/api/2020-11-03/race-page/pennsylvania/president.json
What I don’t know is how this information is gathered and interred into the tally. Is there a human somewhere in the mix or are these taken from a direct feed from the counting “machines”. In other words I don’t know the integrity of the data. Could the vote switching I see be human error or is this “valid” data and these inconsistencies are some of the evidence? If this is good data then the vote switching is simple enough to see that I can explain it to my family over the holiday week…
Any insight on this or other public sources of data you can point us too would be helpful..
I voted, but not for any of the old white guys with valid rape charges against them.
P.S. if you need truly private messaging and data storage in any of this endeavor, you can use mangofarmsassets’ RVN solution. There is a cost in RVN now but with the “memo” function, encrypted private messaging will only cost the transactional costs. If Doug knew that you needed the memo function working I am sure he could have it done in a few days…
Patrick – Thank you so much for coming forward! Just like Donald Trump, you have enough money to check out, play along, and enjoy the rest of your life. But instead, when you see something wrong you use your time, money, and efforts to help the American people. Thanks for everything that you’re doing to get the word out!!
Hi Patrick,
Great job! Are these mathematical impossibilities that would be airtight in court? If so, is it a foregone conclusion with the data Trump’s lawyers have that he will prevail in the courts?
Patrick, can you post more technical data like timestamped logs along with screenshots (even if just for a demo of how adjudication works)? It seems that to prove vote switching, you need to show a higher rate of adjudicated ballots by county. Can the adjudication rate be determined from the ballot machine logs?
wow.. i think God is hearing our prayer.
Patrick has laid bare the obfuscation from the Sydney Powell detractors, and summarizes the fraud brilliantly and in simple to understand terms.
I will have to see what else he has to say about investing… since he may have revelations on that as well.
Let there be justice.
Let us be glad for men such as this.
Is the source for the data used to create all the charts the Edison data used by the New York Times?
That data is available from many different sources. Not just the NYT. That just happens to be one copy of the data. And no not all of this is predicated on Edison Research data.
Thanks. The only data source I see cited for the charts is the NYT.
Would be cool if all the source data could be provided as well, so others can dig in and repeat the analysis.
Patrick you said in an interview a lot of this was stopped in 2016. How was that done and why wasn’t it stopped the same way this election? Thanks
Patrick, Thank you for not being an evil corporate sell out.
I always knew you were pro humanity.
Bitcoin <3 & Freedom <3
Great job Patrick. I first learned about you when I was researching naked short selling a very long time ago. I admire your courage and determination, not only to stand up for your own beliefs, but also against injustice and for the greater good. I can relate to that. I discovered I was a libertarian when Ron Paul run for the republican nomination in 2008. I was following the live stream of the caucuses in the middle of the night from the Netherlands (I am Dutch) and tried to get our national news to rectify their false reporting on how Dr. Paul was doing. I somehow landed here some time ago before the elections, probably because I wondered how you were doing after seeing the great performance of the OSTK share price. I’m very glad everything worked out well for you and that you somehow got some justice, meaning you prospered instead of being ruined. Keep up the good work. In the end, justice/honesty will prevail. It’s amazing that you are fighting this fight even though you really don’t have too. Thanks again.
All vote counting software should be open source
Mr.Byrne ,
glad you enjoyed UK. I spent 2 years working in US ( LA and TX).Loved it. Great people , very generous and fun.
Not sure if you can answer these questions below but might help folks to understand more…..
1. If you expected this computer fraud , did members of DOJ/POTUS also expect and did they prepare for it OUTSIDE of your own organization ?
2. If YES , who would have monitored the steal. CIA ? DOJ ? MILITARY folks ?
3.When this coup is proven how can it be fought and defeated with such massive and obvious corruption on DC (everywhere > MSM, Big Tech, Dems , RINOs , CIA, DOJ(even Barr ?), FBI , Judges(Flynn case) , even Military ? SC(Roberts ?) just who can POTUS and the American people rely to fight this coup?
Can POTUS + 75 M patriots overcome ALL levers of power in the USA ? legally ?
I hope so , but I fear the worst if the SC and US Miiltary are also corrupted.
the Americans I know will NOT put with this under any circumstances and their anger WILL boil over.
The people who instigated this potential for violence are truly dangerous, corrupt , arrogant, desperate and evil.
Answer is yes
https://www.whitehouse.gov/presidential-actions/executive-order-imposing-certain-sanctions-event-foreign-interference-united-states-election/
Patrick
How are those “Fixing the vote” tally charts showing vote spikes in Michigan, Arizona, Georgia etc generated? where do they come from? Why no chart for Pennsylvania? What’s the evidence for the note on the Georgia chart “Backdated Biden ballots”?
I think the ‘siphoning’ isn’t getting enough attention because that is 1) likely more widespread and 2) likely accounts for many more votes nationwide, which is an indicator of the electorate’s sentiment. Thank you for the work you are doing!
Thank you so much for your effort. We must fight the deep state and the billionaire globalists criminals like Soros, Kill Gates, ….
God bless you and your family.
Thank you so much for your effort. We must fight the deep state and the billionaire globalists criminals like Soros, Kill Gates, ….
God bless you and your family.
Straw man argument. Nowhere did I claim that in Maricopa only Republicans were given Sharpies. You just made up that claim and put it on me.
I am open to the possibility it is fraud but I don’t know enough about election data time series to judge whether the “injections” are explicable by some kind of sorting of legal ballots. Do these big spikes occur in normal elections or only in these time series?
Patrick, please read the information on this site: isgp-studies.com
This guy, step by step, explains what happened in Georgia.
He shows the exact batch and moment of the fraud.
https://www.youtube.com/watch?v=mp0u4dw7GH4
Well done that man! God bless.
You need to get this to Sydney Powell, Rudy Guliani, Lin Wood, and Jenna Ellis stat!
Thank you so much for trying to save the one thing we all had/have—-our voice, our vote!!!! Our country will forever be changed if this is allowed to stand!
Patrick,
It is great to see you are back at Deepcapture.com and especially great that you are in this fight. I am supporting (financially) Sidney Powell’s efforts. Just watched your Santelli interview and have a small request — would you mind giving us a heads up at Deepcapture.com whenever you have done an interview (print or video) for the next few days / weeks? I don’t want to miss any of them. Thanks for all you are doing and Happy Thanksgiving.
By the way, is VOATZ owned by tZero (hopefully) or by Medici?
Hi Jeremiah 9:24. I vaguely remember your handle from years ago.
Voatz was funded by Medici.
Yes, have been around for a while, doing what I can. It’s still going on by the way, the big houses don’t seem to give a $#!+ about Reg SHO and still counterfeit at will.
I was asking about VOATZ because I’m a t0 investor (from the R506 at the $8 price point), don’t even know (or really care) what the current price is. I think it’ll be a generational hit at some point. My tokens are still “with” the transfer agent, one of these days I will get around to moving them.
Anyway, God bless and I am very thankful for what you’re doing. As you clearly know, it will help determine whether we remain a Constitutional Republic. I am convinced that we’ll win.
I actually understood this front-to -back and that’s saying something. I really appreciate this work more than words can say
Patrick-
just saw your interview on Mc??. thank you so much for your work on this issue. will follow your site and look forward to your hard-hitting analysis.
Thank you for the info Mr. Byrne. You are a patriot and telling the truth in a world of lies is radical. The only problem I see here is how are these charts going to prove to the SCOTUS that there was a fix? Sure, they can see the numbers on a chart but can the see them on the ballots themselves? I don’t think the SCOTUS will review one ballot. We have to have an individual machine and it’s code showing the fraud. Then we need all the machines in these 5 cities and their code to show all the fraud. Without that, I think we are all like Chuck…
The graphs don’t match the narrative. The graphs are consistent with large ‘bumps’ for Biden when the absentee ballots are counted. The Michigan one looks odd as there is not an apparent uptick in Trump votes when the absentees hit. But the Georgia one shows simultaneous jumps. I don’t know how the API hit but in Michigan you do see a smaller but significant Trump jump after the first absentees hit. Also odd but not consistent with your thesis.
It’s a big disconnect to say the vote in the cities is manipulated and the to show the state data. You need to isolate reporting from within a city to see if there are badges of fraud (like Trump vote dropping).
Big picture this seems backfooted and implausible if you assume as alleged vote counts could be hacked. The simplest thing would be to just manipulate the November 3 in person feeds (eg hack the red county feeds). Also not sure this could be done for counties that have paper votes. Any incorrect tabulation should be caught and flagged in canvassing.
The other possibility for the oddity about Biden jumping but not Trump in Michigan when the absentees hit is that the early batches were sorted, and reported at different times.
But again, if what was done was manipulation of the absentees that wouldn’t be a Dominion thing. And it’s a lot easier to catch. Those ballots exist physically or they do not. Virtually all counties in Michigan voted along the lines of what history and conditions on the ground would tell you they would. The exceptions are that Trump got about 5k Detroit votes than in ‘16, and Detroit turnout was flat. If Detroit turnout was as high as in other counties it would have been more like the six or eight Trump loss most polls predicted. Kent County going blue was a mild surprise but consistent with the polling that Trump was doing poorly with college educated voters. Obama also did well in Kent County. Also Muskegon went Trump, by less than a point. Oakland County also went more heavily Blue than in ‘16. A surprise unless you follow the logic of what happened in Kent and in suburbs across the US. The overall picture in Michigan is that turnout was *really* high in Trump counties or else the beating he took there would have been worse.
Have you, by chance, looked into Bill Gates/Microsoft’s “Election Guard” and his “Defending Democracy” when it comes to this election? Laura Loomer just brought it up on her Loomered website, You might find it interesting.
The wiki style citation links don’t link to anything
Thank you and God Bless you for explaining this to us (the everyday little people) and possibly saving this great Republic! I’ve been depressed for some time about the FBI lack of leadership and the fact that half the country seems to be flying on a different airplane. I was lucky enough to have been born an American citizen. When I see scenes of the lack of basic law and order in many of our large cities it has amazed me how it defies logic and common sense that the inhabitants of those cities keep reelecting the same corrupt, clueless, and narcissistic leaders, My vote is all I have and many have died or sacrificed so that I have that treasure. Please make sure our Supreme Court sees your evidence because we are near the point of no return. Your article explains clearly what has been going on and now I have hope that my fellow citizens aren’t as mixed up as the election results otherwise would indicate.
Thank you for your great contribution to a free Republic! Election results should be thrown out and sent to the House of Representatives for a vote due to overwhelming election fraud shown as you have above.
If I’m understanding the theory correctly, the software provides the answer as to how many fake ballots are necessary (after manipulation like “drop and roll”) and then the fake ballots are created to fill in the falsified numbers. Is that what the theory is? Because without fake ballots, the hand counts would reveal the software manipulation, wouldn’t it? If that’s correct, then it explains why every state where this may have occurred is strenuously resisting ballot signature inspection and a deep audit. I’m not disagreeing with the allegation that there is a lot of very improbable mathematical evidence emerging (like Gwinnet County for example….read Daniel Horowitz’s excellent article on this county). I just think that it’s really important to be able to explain how this was done if it was, in a way that a judge can understand. In addition, the Trump litigation team needs to be able to explain what happened cogently and with great focus (I totally agree that if there was fraud it was focused in key areas, and not widespread). Moreover, they need to seek a very specific remedy…deep dive audit that includes ballot signature inspection.
When can we expect someting to happen to overturn this fraud of an election,
Patrick ~ When this is all said and done there will be heroes that helped to save our great nation. You sir are one of them and I thank you for your in-depth research and clarity into this clear fraud. Many on the left will need to see concrete evidence so they can be assured this was indeed fraud and their beloved Biden actually did not win and Trump actually did not steal anything. Fair minded people will see the truth and the thugs will have to be dealt with because there will be chaos when this gets flipped back to Trump. Those that fight the good fight will be recognized when all is settled. THANK YOU and if I can be of any assistance I am ready, willing and able!
Thanks for sticking your neck out here. US has so much corruption, but so many honest good people like yourself also. God bless you, Sydney and those who haven’t rolled over and played dead in the Republican party. What a bunch of traitors they are.
Mr. Byrne,
Could you please give me your thoughts on this analysis of Michigan’s results? It’s from the Republican blog site RRH Elections: https://rrhelections.com/index.php/2020/11/19/how-trump-lost-michigan/
That Georgia graph on the turnout is money.
COBB County really stands out here.
Excellent work Patrick, thank you.
Digestible info is what’s needed more than ever.
Way to fill the niche.
Thanks. No start spreading the word to all the goons saying, “Where’s the evidence?!?!?!”
You are the definition of the word patriot! Thank you for all you do!
I just want to say “Thank you, Mr. Byrne!” You are a hero! Lots of love from us to you. Be safe!
Thanks Patrick for keeping us in the fight! Just followed you on the TWIT and watched your video with the DR so I came to check it out. I’ll keep checking back now that I know how hard you’re working to keep us informed the truth!
Thank you Patrick! Keep ’em coming until we restore the Republic!
I kept getting flagged posting your website info at DailyWire. By using transposition I was able to post though. Thank you for your work. Those graphs are really important, they really illustrate the point.
Excellent job!
I just wanted to say, from the bottom of my heart… Thank you! You are a hero and patriot.
Hello Mr. Byrne,
Thank-you so much for this investigation. I’m a retired big data processor of 32 years – Relational database, SAS and SQL with microrsoft access, powerpoint and excel expertise. If I can help in anyway please don’t hesitate to reach out. As you’ve stated any time the system numbers don’t match the ballots you’ve got a smoking gun. By chance does the system data you’ve accessed have any location information – postmark location? Mail-in ballots should theoretically be processed close to home – my local post office. If large ballot dumps occurred late 11/3 to 11/5 I wonder if they can be isolated to not only a city or town but the local post office as well. I also wonder if there was a process to compare walk-in ballots and pre-processed mail-ins to voter registration information. If so – late 11/3 a quick query may have been run to identify those who DID NOT vote. Assume mail-ins for non-voters were system generated (paper or system) based on walk-in only voter info (late 11/3) since the existing true mail-ins may not have processed. This could account for the excess number of mail-in ballots – theoretically duplicates should exist.
Keep up the fight!
Thank you for your tireless hard work! This nation owes you a huge debt of gratitude for all that you are doing. I hope that people will listen now! We need more fearless Patriots to keep the wolves from our doors. My generation did not do their job keeping an eye on our Great Republic, we will do better.
Thank You, God Bless
The PA ballot totals are off. PA had reported receiving 2.4 million ballots prior to 11/3. https://www.pennlive.com/elections/2020/11/more-than-24-million-mail-in-ballots-have-been-returned-in-pa.html?outputType=amp
I was a kid at a party. 20, 21 maybe. The girl’s step dad was a Philo Prof at the University. I asked him where all the smart people had gone & he replied “in hiding. It’s too dangerous to be smart” & I should “go find some weed for him”.
I bet you get less invites to parties than I do 😉
TY for your light. From Canada.
Thank you for your excellent work sir.
From a black gal patriot who loves her country!!
Pat, get this over to War Room Pandemic with Steve Bannon and blow this up.
https://pandemic.warroom.org
I’ve wanted Patrick and Steve to get together for a long time to discuss many topics. This voter fraud would be a good place to start.They have a lot in common personally as well.
Yes I agree, many similar manerisms. Both have nuclear reactor ‘Brain’ power.
Outstanding! YOU are a great American and a fellow ardent patriot! You get it…we either fight and win or we no longer have a country…I am with you
Veteran US Army
“Pennsylvania reports having mailed out 1,823,148 ballots, of which 1,462,302 were returned.”
Where did you get this number?
Boockvar noted: The state approved 3,098,947 mail-in applications and confirmed 3,082,832 for mailing.
I found the same thing way above 2.6 million were sent out.
It seems likely that PB’s number is in error. I quoted it, was challenged on it and also find that enough ballots were mailed out to cover the number voted and unreturned. No source is cited for PB’s number so what is it?
The graphic is fraudulent. See
https://www.deepcapture.com/2020/11/election-2020-was-rigged-the-evidence/#comment-1128648
Very good data. However, I’d like to point out that it seems to me that your Michigan graph looks more like what happened in Georgia and viceversa. I remember that on Nov 4th morning Biden took the lead in Michigan, whereas in Georgia it took him several days. Please clarify if this is correct. May the truth prevail and justice be served. Thank you.
Cheering you on from Canuckistan! Thank you for this patriotic work to uncover this lawlessness.
Thank you for your hard work Patrick! America first! Have you looked into election results from CA, NY or any other really blue state? From what I see in a southern CA major city, there are way more red votes than show in the election results.
Election results should be fair and transparent while giving the voters what they want. God bless.
Thank you for your hard work Patrick! America first! Have you looked into election results from CA, NY or any other really blue state? From what I see in a southern CA major city, there are way more red votes than show in the election results.
Election results should be fair and transparent while giving the voters what they want. God bless.
do you have the datasets for this saved? I’d like the data per day as a CSV at a state level and county level in 2 separate sets?
I found some data from a forecast , but that forecast seemed to have the votes in percentages…
Thank you, Mr. Byrne, for your efforts to protect our country’s rule of law. The charts here make the anomalies very easy to visualize. As someone who must be quite familiar with the tech space, I am curious about your thoughts on the involvement of big tech companies – Google, Facebook, and Twitter – in driving the public narrative pre, during, and post election. What’s likely in it for them?
Also really loved your philosophical talks at the Misus Institute. Big fan.
Thank you for your work on this!
Thank you for all the work you doing! God bless.
It is hard to assess here exactly what the mechanics is for the manipulation. These are serious charges and the particulars should be set forth as clearly as they can be. One of the videos linked above, and some of Patrick’s comments, propose that there are implausible patterns in how large amounts of votes (absentees, once counted) appear in huge lopsided chunks, and then in oddly coupled set patterns (50.05, 49.95, e.g.). Where is that data drawn from? If the source API is feeds, is there information for how Edison obtains and reports the data that could contextualize (or confirm) that there are indeed anomalies? If what is observed is the API, that is coming not first from the reporting precincts, but from Edison. On the days following the election, I followed the AP state wide vote reports from Pennsylvania and Georgia as they came in, sometimes several times an hour as the AP feed was automatically refreshed. The votes would come in batches of anywhere from a few hundred to ten thousand or so. In Pennsylvania, the batches were always between 55% to 80+% Biden. For Georgia, from 50% to 70+% Biden. It was not 100%, 50/50%, or otherwise “dump and roll,” at least in terms of how the votes appeared to be coming in at the time.
Freedom was granted to us by God, it is enshrined in our Constitution. Protected by people who put their lives at risk in our military and as private citizens. Thank you, Patrick
After your “Message from deepcature” popup, hit “agree”, and 502 web error is returned, locking the page.
After your “Message from deepcature” popup, hit “agree”, and 502 web error is returned, locking the page.
You are a Patriot! I admire & am akin with your Fighting Spirit!!!
Patrick,
One of your Silicon Slopes VC associates here… posting anonymously for obvious reasons. VC is a cesspit of conflicted interests but some of us understand and applaud what you are doing. Please keep fighting and know I’m forever thankful.
Patrick Thank you for being a True American Patriot.
Patrick,
Thank you for this great work! I’m going to have to read this a few more times to fully digest this material. Quick question, the various ramps you show in various states that essentially put Biden on the path to victory, do they all occur at the same time (potentially indicating, an automated feature), or are they sequential in time (perhaps, indicating manual intervention)?
Patrick,
Thank you , Thank you for standing up for America!
I appreciate you man…I appreciate your sincere efforts
God has His plan and I think you all are a solid part of it.
Time to lower the BOOM my friend!
Hello Patrick,
Are you looking into California as well. The media called CA less than 10 min after the polls closed.
Thank you and God bless you!
Hello Patrick.. I’m in New Zealand and do my damndest to keep abreast of what’s happening so I can help others understand. Thank God you took the action you did and started educating key people about the source of what many of us believe to be the worst case of election fraud ever. You are writing history sir and I applaud you. Thanks on behalf of millions of other concerned people worldwide.
Hi Patrick,
I’m also an experienced data analyst. I have a lot of analysis that matches what you’re saying however, I keep getting stuck on one issue. How do they get past the printed paper ballots that are created with every vote by the Dominion machine? If the machine votes opposite to what the printed paper ballot says (which matches the voters’ selections), don’t those differences get picked up during a recount (and potentially by the voters themselves)? Do they just generate votes on the spot along with the accompanying printout when they spike the votes at night for Biden? How do they identify just the Trump votes to throw out (which I assume means they have to throw out the matching paper ballot printouts as well)?
I do know about the rejected ballots scheme (where they set up the machine to reject ballots in Trump counties for bogus reasons so they can be inspected by hand) but that would involve manually rejecting the paper ballots on inspection. What you’re talking about and many others have discovered are electronic manipulations of votes. But how can that be done if there is a paper trail?
If a ballet goes to adjudication, a new ballet is printed with what is the voters “intent”. That ballet goes in the box. The problem is that it appears mass adjudication was done without both parties present. I watched all the testimony from all the swing states on OAN. I heard pieces from many people that connect the dots. One being hundreds of pristine ballots, no folds all for Biden. I also heard in Detroit a poll worker of 31 years describing a piece of correction tape placed on the tabulator. A single Dominion contractor did this all day on 11 tabulators. What this did was send all the ballets to adjudication but it contained the QR code as the tape didn’t cover the entire row. So you have the QR code to match the newly printed ballet that can be matched with the envelop. The newly printed ballets were then tabulated. By law the adjudicated ballots and all images were supposed to be kept for 22 months. A forensic audit could prove all ballots printed by adjudication vs. hand filled out with a pen. Large numbers of printed ballots would prove fraud. Additionally we would see a lot of messed up ballot images. Another testimony told of tabulators stopping because they were “full” of ballots. The memory card was removed and the ballots were transferred to another drive and taken someplace. The card placed back in the tabulator and it was fast again. I also watched the entire 1 hour training video Dominion gave contractors on Nov 2nd 2020. In that video the training person stated there were 20 tabulators in Detroit at the TCF center and 13 adjudication stations. If your only rejecting 1 of 125,000 votes and processing a few thousand military ballots, why do you need 13 adjudication stations. Which nobody was able to see or witness.
Patrick – I’m sure the election was stolen. But if I’m understanding the data feed correctly, I also think there are rounding errors here that are not accounted for. I would suggest you explicitly tackle this in your analysis.
I very much appreciate your analysis and time. Without you and Sidney and the others, I think I’d be going crazy.
Thank you so much for all you are doing to expose this fraud. May God bless you!
Look at this point it doesn’t matter whether you’re a Democrat or Republican it doesn’t matter if you are gay lesbian transgender whatever. If you love this country open your eyes and see what’s going on! They’ve been doing this for decades they’ve been lying they’ve been cheating they’ve been stealing all across the world not just the presidency. The down ballads the Senators the congressman the Pelosi’s the tumors call Ryan’s of the world. Put your despain aside for president and open your eyes as an American he’ll open your eyes as a human being and understand that this is the greatest scam deep state has committed against the American public in the last century
Are there typos in that table of PA votes?
When I add up the two rows, I get Trump with 9570 more votes than Biden: 3465578 Trump vs 3456008 Biden.
I’ve seen a number of analyses showing the Steal via math, but none of them were valid, in my estimation. Here on this site, however, it looks like you might actually have a thing or two! Very much appreciated!
Pennsylvania official votes (@11/24 8 PM) was the heading of that table, so I believe it took Biden’s number several days before it surpassed Trumps.
A little more math reveals that 11/24 is, in fact, 21 days after Election Day. 21 being more than “several”.
Not enough “proof.” Satan holds on like grim death because he is “grim death.”
Some interesting items here:
https://www.frontpagemag.com/fpm/2020/11/why-trump-will-win-joseph-hippolito/
BRAVO!
You have renewed my hope in humanity.
Patrick,
You’re a true American patriot and I can’t thank you enough for this incredible work you’ve done.
I am praying that your work will bring this fraud to light and expose these injustices to the masses.
We, the American people, have witnessed the fraud on the day after the election but didn’t understand how it could happen until you showed up and we are beyond grateful for your generosity in taking this on.
Thanks for some great work Patrick – I am quoting these stats all over the place.
I have a query (not a challenge) about the whole USA data that was being shared throughout the night (PBS) – the summary of which is:
After 101m votes counted at 23:26 hrs. (ET) on 3rd November (night of election) – there was a reversal in Trumps fortunes of some 3.8m votes.
He was leading by 3,552,157 votes at 23:00 hrs. but then went into a 308,202 deficit at 23:26 hrs.
Is there a logical explanation for that change?
Many thanks again for your work
Start making cash online work easily from home.i have received a paycheck of $24K in this month by working online from home.i am a student and i just doing this job in my spare time and i work daily 2 to 3 hours a day.everybody can join this job and make extra income
PB live https://www.youtube.com/watch?v=1NnUsUBD4FY
Since when do ballpoint pens need to dry, am I missing something.
I didn’t read any evidence of a rigged election from your analysis, only ways in which the election COULD have been rigged (as well as some associations with controversial characters).
It could have also been rigged by everyone having their brains swapped for a different brain. Please add that possibility to your analysis. Thank you.
As other posters responded, the PA numbers of people mailing in voting matches PA State website (not 1 million additional people). I even thought the state website could (would) have reflected the additional people (just to balance), so I went to TargetSmart Early Voting page and for PA, it does show a daily chart of mail-in submissions that get up to 2.6 million on election day (they were collecting data along the way).
Now, if you want to question the break-out, you show 600k voted for Trump and 2.0 mill for Biden. PA reported the breakdown of who voted as 1.7 mill Dems, 623k Rep and 300k Independents. Is it feasible that Biden got all the Independents?
Be cautious of 1 million vote swing as that kind of fraud cannot be easily covered up. And, if your computer geeks have time, a good chart is the GA change in turnout plot by districts but do it on counties all across America … if you are right, the 5-6 cities/counties should stick out like a sore thumb. I have heard this before, but no one has shown the data to be verified.
Lastly, the reason for the big spike in Arizona data (at the beginning) is that Arizona allows its BOE to start counting early mail-ins days before. Thus, there is a big dump of those votes right at the beginning as the counting is already done (but cannot be reported till after polls close or its a felony). Others states dump it later as their rules are envelops cannot be opened till polls close (or that day) – long process. But, for Arizona, this is not an abnormal spike as it was tallied before polls actually closed and then sent out. (Allowed per their rules)
And, most mail-in ballots would (could) favor Dems (as early national pre-polling was showing by 2 to 1 at times — as Trump voters waited to vote in person). The hard part is trying to figure out who actually did as polling was so far off (in Arizona, the final early voting was close to 3/8-3/8-1/4 Dem, Rep and Ind for the state). So, Biden jumping out ahead is a little suspicious there if we knew how the Independents split in those 2 counties (even between Dems and Rep? If so, then it is suspicious that Biden had 12% lead early on when it should have been closer (but not the fraud you talk about — shutting down everything to figure out how much to add in the middle of the night).
Good luck … some things are very off but other anomalies can be explained. Fix it early before the media locks on to one of two that can be fact checked easily to discredit you.
This video has been censored by YouTube. It shows vote flipping caught on dominion voting machines. Almost every time I share this, it gets deleted so I am attempting to share it again here. https://www.youtube.com/watch?v=ztYDXWRLVI0&feature=youtu.be
Really great catch. I am going to see if I can find a data feed to back this up.
Just did a little digging and WOW!!! found https://results.enr.clarityelections.com/GA/105369/web.264614/#/search?
Clarityelections.com is mentioned in the video as providing the data feed to the AP.
But if you remove everything after the .com : https://results.enr.clarityelections.com/ you get redirected to!!!!!!!!!!
https://scytl.us
So somehow Scytl, who had there servers confiscated in Germany is connected to Clarity Elections.
God bless you for what you’re doing. We have been feeling helpless, angry, scared and so concerned for the very future of our republic. What you are doing gives me hope that this terrible attempt to steal this election will be exposed and reversed!
Patrick: Thank you very for your patriotic service to the country. We have to STOP THE STEAL. God bless…
Urgent – MN has a video proving voter manipulation/deleting/etc. Based on open data. I want to get it to Mr. Byrne or a right hand – it was done w/ 3rd party votes BUT the logic could apply to any subset of votes. SO, will someone please contact me via email required before comment.
I know this is open but there has to be a way to get info to him. VERY impt.
Mr Byrne,
How can citizens help?
Please point us to how we can assist. Money? Share this info? Any other actions?
I’m sure Oathkeepers will offer you round the clock protection if you need, or ask. Some of us have “interesting” former military qualifications to help keep people like you safe.
You should definitely give your money to Patrick, a man who’s dad is worth hundreds of millions of dollars and who just last year sold 30 million dollars of stock. If you have money laying around to hand out give it to a food bank and actually help some of your fellow Americans.
Patrick has already made it clear to help Sidney Powell because her legal efforts are entirely self-funded. She is focused on exactly what Patrick is bringing to light and he is feeding her information – they are a de facto team of Super Patriots. I gave, care to join me? https://defendingtherepublic.org/
Patrick, is Cuomo going down with all of this? I pray.
Haha – if not, he should be.
How can I share this article? There is no share button.
Patrick, where do you find the 1.8 mil Mail ballots were sent?
I can find reports of 3 mil requested, and 300k refused applications, but I don’t see a total actually mailed…
Of course that’s typical bureaucracy….. some returned before sent date that also doesn’t make sense.
So true, we lose this and never another free election. I am grateful for your work! God Bless You!
Note.
I had posted your charts and got some feedback from some people.
They said
1)
https://twitter.com/Stigni/status/1331574932275417088?s=20
Davide Galliani
@Stigni
·
4h
At the 01:14 am (ET) the DeKalb updated the 84% of his Advanced votes (163k), at 01:31am Cobb update some of his Adv votes (35k).
At 01:35 am the SoS Website was updated, and at 01:36am the NYT website was updated.
It’s just a big batch from a blue county: https://results.enr.clarityelections.com/GA/DeKalb/105414/web.264614/#/detail/1?v=271880%2F
2)
You realize that they don’t input votes one at a time, as with mail in’s they are uploaded in batches, rather large ones because they go through tabulation checks before officially submitted. Is it REALLY this easy to fool minions with pretty pictures? Apparently so #ByeDon https://pic.twitter.com/jLvPMp5IyI
There is work to be done with the counties that provide voting data by voting type (direct versus party-line). I did some work with Michigan data and the patterns look very odd. For example, across precincts, the % party line vote is higher and more consistent for trump than biden, who has substantially more variability (less consistency in voting style across precincts). The more you dig, you’ll find trends in voting style differ substantially for biden (both in average % and variability in voting style) depending on the degree to which the total votes differ between trump vs. biden. However, when you do this for trump voting style stays consistent across precincts regardless of the vote differences between candidates. In other words, it looks like there is some evidence weighting going on (i’m guessing by a combo machine, dumps, and other stuff) that can be picked up because dataset includes voting type… The more trump was winning, the more direct votes for biden – weighting lessens as biden is winning more.
None of this is ‘odd’ in a contested election in which independents swing towards the opposition candidate.
That Republicans cannot fathom the idea that independents research their votes and vote for the person they feel best suited to do the job or don’t vote for that race at all is quiet telling. Now this is highly anecdotal but I’m a big believer in microcosms, and of the Trump voters I know, every single one of them bragged about a straight party-line vote.
So it makes sense to you that in somewhere like Kent County, MI, if you take precincts of roughly the same size and biden win’s one group of precincts by 15% and loses another group of precincts by 15%, the expected number of direct votes would be about the same in the two precinct groups? That is what I am seeing in the data and it doesn’t make sense. In every other condition both direct and party-line votes correlate with the total differences between candidates (e.g., when biden won bigger, he also got more party-line votes; when trump won bigger, he got both more direct and party line votes). If you or anyone else has thoughts on this, I’m honestly interested in learning more. I am struggling to understand these patterns in the data.
I think a big problem with trying to discover election fraud by analyzing for anomaly in the data is that you’re assuming incorrectly that people vote rationally and in distinct patterns. It’s the same problem in economic theory in my opinion: that when studied at scale, people act rationally. Again, anecdotally, I just don’t believe that to be true. I believe people, at scale, act more like herds of cattle, and that includes following the herd right off the cliff.
So the ‘pattern’ of votes here might just be that among friends and families in suburbs like Grand Rapids, Trump lost a lot of voters from 2016. My hunch was always that he only actually won in 2016 because a slight majority of undecided voters who didn’t really care for either Hillary or Trump said ‘f* it, i’m voting Trump lets see how it goes’. I think those same voters decided they had had enough of the reality TV show presidency but might have kept voting republican elsewhere.
Also what I’ve noticed in this and similar theories is that they don’t seem to be taking into account that in many areas of the countries, Republicans and Democrats run unopposed. That would mean that in these races, disaffected voters who want Trump gone and don’t much care for the party that has rubber stamped his lunacy would only vote for Biden and not give any of the unopposed republicans on their ballot the benefit of the doubt and abstain from voting in those races. I don’t think anyone is really accounting for that in these theorems here.
Seems to me you went into this with a premise, ‘the election was stolen’, and then looked for any data that appeared to match this premise.
The biggest flaw that I see here is that you’re simply discounting the idea that the majority of mail-in ballots were for Biden. I think its pretty reasonable to assume that would be the case given the attitudes towards the pandemic between Biden and Trump voters.
The other huge flaw is that you’re using the ‘reported votes’ data stream. Votes are counted and results batched and then eventually reported. The Occums razor scenario here is that large swaths of mail-in ballots were counted in heavy Biden districts and then batched and reported in a couple of large swaths. Is it really THAT unlikely that as shifts changed, people went home or took breaks in the early hours that batches of mail-in votes were being collated but not reported until a big push when the counting started ramping back up?
Sure sure. 600,000 mail-in ballots processed in a batch, 3,200 for Trump, the rest for Biden. Oh, and it was in the three hour window that goons kicked observers out, water-mains break, goons block observers, tape newspaper over windows, and carry in backpacks while gooning any remaining observers.
Nothing to see there, move along….
Thanks for your work, Patrick! I have a question about the claim “Pennsylvania reports having mailed out 1,823,148 ballots, of which 1,462,302 were returned.” I repeated this on FB and was called on the 1,823,148 ballots mailed out number. I looked into it and the best I could find were news articles in October referring to 2.6 million or 2.8 million ballots requested. So I would assume that by election day the total would be close to 3 million requested and something close to that mailed out. In your claim you cite no source, and the number seems to be in error. Could you check this? I know you want to get it right. Thanks again for all your work!
“Seems to me you went into this with a premise, ‘the election was stolen’, and then looked for any data that appeared to match this premise.”
That is exactly how a fraud examination is supposed to go, Fraud Examination 101 instructs you to take a “worse-case scenario” hypothesis before you even start pulling data and then you can revise and amend your hypothesis as the investigation evolves. Starting an investigation requires predication, and an investigator has to always assume the case will end in litigation which is why you will begin with the premise not only that fraud occurred but that the worst possible fraud scenario occurred.
A little more math reveals that 11/24 is, in fact, 21 days after Election Day. 21 being more than “several”.
People Must Stand United in Purpose for Life, Liberty & the Pursuit of Happiness. But, it’s your Choice. Gather Together Now In the Physical because to Lay down & take is death. For God has not given us a spirit of fear, but of power and of love and of a sound mind. Act in Faith.
Patrick,
On the Michigan Graph, I see multiple times prior the Digital Fix, I see injection for Donald Trump twice and Joe Biden once, I am not sure if someone has seen this, but a look at the graph overall, it seemed like injection happened for both candidates during early Nov 4 as well.
Do you see it the same way as I do? Do let me know your comments.
Regards,
Som.
Patrick,
Thank you again for all you are doing.
As others are pointing out, Bev Harris is a very useful person to point outand perhaps to contact. I participated on her Forum before it was destroyed, it had a huge archive of what is going on right now.
“Nothing new, under the sun.”
I think one of the sad parts here is how many may few this all as new or just having happened. The fact is this has been going on for a very long time. Here is an example of remote access and the fraction magic others are pointing out (note the dates):
https://blackboxvoting.org/fraction-magic-part-6/
“In Pima County, Arizona, it was revealed during litigation that a technician was making copies of the GEMS election database and taking it home overnight, then loading it back onto the official computer in the morning.”
“Perhaps the greatest access of all goes to the big boys, the four major vendors for election equipment in the world (ES&S, Dominion, Smartmatic, Hart Intercivic).”
“The following excerpt, taken from the deposition of Shelby County Election technician Dennis Boyce, 23 demonstrates that vendors are sometimes provided with remote desktop access during elections.”
“Well, Mr. Underwood looked at the data and we had a remote session with WebX and he looked at the data and looked around. We told him what happened and we told him that we needed to resolve the issue. And he looked at the data and they did their little deal or whatever they did to correct it and told us to reconfigure the data again. They kind of reset stuff.”
And more, Spain / SCYTL: https://2012patriot.wordpress.com/2012/05/07/george-soros-counts-presidential-votes/
Keep in mind, I recall Bev stating this but I can’t find her post, I’m just using that article because it confirms my memory of what she said:
“And although the votes will be cast in hometown, American precincts on Election Day, with the Barcelona-based SCYTL taking charge of the process, they will be routed and counted overseas.”
“But although SCYTL’s self-proclaimed reputation for security had won the company the Congressionally approved task of handling internet voting for American citizens and members of the military overseas, upon opening the system for use in the District of Columbia, the University of Michigan fight song “The Victors” was suddenly heard after the casting of each ballot. The system had been hacked by U of M computer teachers and students in response to a challenge by SCYTL that anyone who wished to do so, might try!”
So again this has been going on for some time, Bev Harris did fantastic work but never got the traction that seems to finally be happening. If these early researchers were brought on board, and their knowledge shared ago with the very long history, it will be hard for most people to deny and not see the crime that is happening here.
Thank you again for all you are doing!
Charles
Democrat Desperation breeds Carelessness. It’s pretty obvious they lost it when they realized their initial efforts would not offset Trumps Lead…so they got greedy, stupid and careless with their methods. Time to hang some Democraps! I’ll personally pay for the Gallows and Rope for all Video Rights, when I sell those the money goes directly to our True Hero’s in this great country!
Patrick, I’d like to offer my assistance to your efforts, if it would help in any way. I’m a pretty smart mechanical engineer. Not a computer techie by any means, but if you think you can make use of another good brain, please reach out. My email address looks bogus, but it’s real and I check it.
I just saw you on OAN – great stuff. Keep up the good fight. Evil never wins. Texas is praying for you.
WHY do CNN MSNBC CBS VIACOM AP DW PBS NPR ETC….all say and repeat the mantra there is NO evidence…never showing or alluding such “false” claims…That MSM media also claims that there is NO scientific evidence…why is even ACADEMIA scientists university professors;;refusing to debate this statistics…NO such thing as FORUM for elections data…the (se)election of Biden defies all rational, logical, mathematical statistical scientific LAWS..Biden is not the legitimate president HE IS A DICTATOR..
Patrick, in an interview today, said he would start posting evidence tonight.
Patrick,
Is the raw data for the graphs available for download?
I ask because I’m getting pushback from others, many of whom are sympathetic to the proposition of election fraud, who say that while the graphics are pretty, we can’t se the data upon which the graphs are based…
It is unlikely that these folks have the ability to perform the analysis, but having access to the information would go a long way in discounting claims that Sidney Powell is a “conspiracy nut”.
The last point- this summary, given your credentials, has raised my spirits…
Providing access to this information would go a long way in doing the same for others…
Thanks for your efforts,
I’ll finish with a pseudonym- just in case things go sideways, to make things a little more difficult for the thugs
😉
Patrick Please Please Please! Checkout this video they mention you A must watch regards Tom D
https://www.youtube.com/watch?v=9UGFFnJuwas&feature=push-prem-sub&attr_tag=PBQLMCIGPIZ-F6dY%3A6
Great video. PB and Sidney must watch this. I have been worried about the court case and here is the way to go directly to the SCOTUS and argue the election fraud violated the 14th amendment
Patrick check this out Please! https://www.youtube.com/watch?v=9UGFFnJuwas&feature=push-prem-sub&attr_tag=PBQLMCIGPIZ-F6dY%3A6
Patrick,
A very humble thank you from an average American with an EE degree, and a life time of looking at graphs and spreadsheets.
You are a true patriot, a true-blue American entreprenuer giving back to your country.
Please let us know what, if anything, the millions of Trump supporters who know in their hearts this election was rigged in just a few counties in the swing states that could tip the electoral college to Biden, can do to assist your efforts.
All that is at stake is the ability to have free and fair elections in our country from this day forward.
We will not submit, we will not go quietly, and if this election is stolen, Hell is coming for breakfast.
They are scared now. It’s a dangerous time. They’ve tried demoralization for five VERY long years, yet we didn’t cave. We knew they were wrong. They’re more wrong now & we have a lot riding on this~ Our Freedom & Our Nation. Patrick (what an apt name!), and several thousands of honorable Patriots have courageously come forward & put their OWN safety second to the importance this ELECTION. Gratitude doesn’t come close to describing my emotions… Love, Respect, Honor… We MUST NOT FAIL~ Bless You ALL! *¤°•.。✮⋆✞︎☆❈★¤
Thank you Patrick! Much appreciated. I would like to point out, however that the PA mail-in vote chart reflects mail-in ballot requests for the PA Primary earlier in the year. I want this graphic to be true, but they sent out more than 3 million mail-in ballots for the General election. 🙁
What is your source Duane?
Here is the site with the figure that is listed as the “ballots sent” in the graphic – the numbers match exactly:
https://data.pa.gov/Government-Efficiency-Citizen-Engagement/2020-Primary-Election-Mail-Ballot-Requests-Departm/853w-ecfz
Here is an MSN article from Oct 19 saying that 2.8 million ballots had been mailed out for the General election:
https://www.msn.com/en-us/news/politics/pennsylvania-mail-in-ballot-requests-hit-28-million-including-700000-gop-voters/ar-BB1abBxM
Here is the mail-in ballots tracked by a 3rd party, as the General election data is not currently available on the PA government site:
https://electproject.github.io/Early-Vote-2020G/PA.html
I think the other evidence is damning, but this will be the one point the Democrats will continually harp on saying that all the other data isn’t credible. We don’t need to give them that opening.
Here is the PA.gov site that the sent ballot count above apparently comes from – it clearly says “Primary” in both the link and throughout the page:
https://data.pa.gov/Government-Efficiency-Citizen-Engagement/2020-Primary-Election-Mail-Ballot-Requests-Departm/853w-ecfz
Here is an MSN.com article from Oct 19 that discusses 2.8 million mail-in ballot requests as of that date:
https://www.msn.com/en-us/news/politics/pennsylvania-mail-in-ballot-requests-hit-28-million-including-700000-gop-voters/ar-BB1abBxM
Here is a 3rd party election data site that shows the number of mail-in ballots for the general election in November:
https://electproject.github.io/Early-Vote-2020G/PA.html
There is plenty of evidence that we don’t need to make these types of mistakes for the fraudsters to point out. It’s all they would discuss and use to try to shut down the argument, saying “you had this one dataset that was based on false assumptions, so we are disqualifying all your “evidence” as being based on false assumptions”.
Tried twice to answer. https://electproject.github.io/Early-Vote-2020G/PA.html
Looks like we also have an NBC affiliate reporting 2.8 million on Oct 22: https://web.archive.org/web/20201022015952/https://www.nbcphiladelphia.com/news/politics/decision-2020/pennsylvania-mail-in-ballot-requests-hit-2-8-million-including-700000-gop-voters/2567670/
The PA mail-in data was scrutinized in this thread where where someone revealed day-by-day ballot counts from a non-public subscription service name targetsmart. It’s worth a look.
The thread heats up with the accidentally confused primary results—ouch.
Then moves to the 3M listed in the U.S. Elections Project Data github data—suspect for PA only.
Then slows down after the comprehensive data showing 2,383,062 requested ballots in the targetsmart data.
The targetsmart and the U.S. Elections Project Data agree very well except for the final PA figure figures which they source from the secretary of state with no link, unlike the other data which seem to all have links.
That’s a bit of a rollercoaster ride, but the result is that 2,383,062 is the most reliable number for the a final vote request count in PA and it would be difficult to make the case that more than 90% made it back in any legitimate way. That of course gives the win to Trump so it’s not going to be accepted easily.
https://twitter.com/MishGEA/status/1331736188353277952
@PatrickByrne : Just found this video on Rumble, posted initially on Nov. 20. Depicts switching in some precincts in PA, using data from the NY Times data feed. Perhaps you need the publisher of the video on your team?
Have a quick look, and Happy Thanksgiving!
https://rumble.com/vbas2t-smoking-gun-dominion-transferring-vote-ratios-between-precincts-in-pa.-by-e.html
I think this “smoking gun” is faulty.
Here is an example of what I think the video maker is seeing:
Consider the ratio 5/61 (for example). I didn’t count, but I think there are something like 500 precincts in the data. So maybe 8 of the 500 will have a vote count divisible by 61 (500/61 is about 8). And there’s not that many options for the “5” count in the heavy Biden districts, so say 2 of the 8 match this also.
This occurs at the start of the data (first big dump). Then the video maker sees the same data reported for a long period, with minimal global changes (IIUC). But at some point there *is* a big dump, and many ratios get changed throughout the dataset. These are essentially a new randomizing factor: so again 1 or 2 precincts might have ratio 5/61 as above. The last timestamp before the big dump, and the first one after it, will then have the “vote ratio transfer” as the video maker claims. While I would say it is just patterns that you would expect in sufficiently voluminous “random” vote data (where “random” means with respect to the voting distribution, eg 85%+ for Biden in some places, etc).
A way to disprove it all is to consider some other similar state, with their data updates, and see if the same “vote ratio transfer” occurs. I would guess it is nothing more than the expected behavior.
The guy recently posted a second video “Smoking Gun, Part 2: Ratio Transfers Proved; Entire Algorithm Reversed, net 200,353 votes for Biden”. https://www.youtube.com/watch?v=3pVAKm8JqvU
What do you think?
Finding an algorithm that generates the voting pattern we observe would be surely the most striking point to prove systematic fraud. Maybe a great task to put a reward on at the data science competition platform Kaggle!
Patrick,
Thank you so much for your work. You are a true patriot.
I will never vote again until this sham of a so called American voting system is cleaned up and the people involved go to jail!!
Thank you for exposing this corruption! I live in WA State and this idiot governor inslee should have never been voted back into office and Trump should have won WA.
I think the smoking gun here is that anytime you see most spikes, even if they favor one candidate over the other, there is a simultaneous spike that suggests mail in ballots introduced or the like. Where it gets odd, especially in GA or MI is that the spike favors exclusively one candidate. In this case Biden exclusively, and days after the voting has stopped. You expect to see spikes, but spikes that affect both candidates. Keep up the good work. We’ve got a country to save.
There is no smoking gun here. The graphs introduced by Patrick, without context or analysis, show the mail in ballots in most states favored Biden. What’s missing is an objective consideration of the data. Are there narratives that explain the graphs? Yes, there are. Arizona absentee ballots favored Trump, as most likely vulnerable elderly people voted absentee and favored Republican. In Wayne County, Philadelphia and the suburbs, Atlanta and the suburbs, the absentees favored Biden.
There was a time when the conspiracy theories Patrick pursued pushed America to a deeper truth. He had real data to support the contentions, such as failures to deliver clustering to certain companies, OSTK in particular. Eventually, the SEC took action. This stuff is a dead end.
You think Trump doesn’t have it all? Think again. https://youtu.be/QrhZ9nnrDr8
Exactly.
Also, I noticed that Team DNC is already filing their Civil Rights lawsuits as you predicted. Total shocker. And who has been assigned but our good friend Emmet “bludgeon Flynn” Sullivan.
Both sides play hard. That’s the nature of democracy. If this is anything other than hot air—this election fraud—it warrants full consideration. And a federal investigation. If this is kvetching you should see how it can be taken as an excuse to suppress voting rights. Vitally important that accusations such as Patrick makes here get tested. For the benefit of everyone.
Patrick Byrne has a history of b.s.
https://www.sltrib.com/news/2019/09/01/overstocks-ceo-made-big/
https://whitecollarfraud.com/overstock-com-accounting-fraud/
To be fair, he also has a history of identifying systemic problems or weaknesses in complex systems, like with the potential to manipulate stock prices through persistent fails to deliver. I personally think his case was overblown (or even flawed, on the merits) with respect to OSTK. But I have heard even his adversaries from those battles say he is an “American hero” (a description I’d debate, but with securities and block chain he is at least directionally correct) for fighting that fight.
I am at a loss to understand Patrick’s loss of objectivity or perspective here. With the naked short selling stuff, he would present the other side in a fair manner. And then point out why the situation still called for SEC action. No other voice was as persuasive on those points–and what was effective was in large part the engagement with the other side’s position.
Having follows DeepCapture for 10+ years and having openly disagreed with PB on certain points I find your conclusions complete baseless.
How do you present the “other” side of vote rigging? Are there defenders of the voting process that are presenting rational argument backed up by data? Is anyone presenting any reasonable alternatives to the conclusion reached by following the evidence.
If you have a reasonable counter argument please present this.
As far as OSTK case being overblown. 200+ people went to jail. $6 billion a day was in counterfeit securities as calculated by and outside expert. How big does it have to be for you?
hello
Quite obvious you have never been an officer in a publicly traded company.
And how many CLEAN SEC audits does a company have to have to not be b.s.
Have you read the filings or the SEC reports? Or are you just going on what a blog poster put up?
Can’t read the first article as I am not subscribing. Based on the date it might have to do with PB selling his OSTK stock. He did not make big and he is not a billionaire. If you read SEC filings you would know this
Patrick
Has anyone looked at Minnesota Congressional District 2 (MN CD2). Small potatoes but our candidate, Tyler Kistner, was leading all day and then a 3 am ballot dump of 8,000 gave Angie Craig the lead and supposed win.
I’ve read posts, you are a one man show and I deeply respect that, you will never know how much…
I’ve heard 195,000 Trump votes were switched to Biden in MN, why wouldn’t that be down ticket too?
It seems that access is now blocked to the “open data” previously available at
https://data.pa.gov/Government-Efficiency-Citizen-Engagement/2020-General-Election-Mail-Ballot-Requests-Departm/mcba-yywm
Is the original dataset available?
https://data.pa.gov/browse
“Pennsylvania Data Assets
As counties finish counting ballots and move toward certification of election results, they are no longer regularly updating the unofficial informational dashboard. Therefore, we are removing the election data assets from the Open Data Catalog. For accurate and up-to-date information, please visit: https://electionreturns.pa.gov/”
Why ever remove open data? (Rhetorical question)
The previously-open Pennsylvania 2020 General Election Ballot Data that was recently removed/blocked by the Commonwealth of Pennsylvania was preserved and is being mirrored by a private citizen. See https://www.dolthub.com/blog/2020-11-09-debunking-election-fraud/#Update2
Thank you Patrick, incredible work! Those graphs of the states that show ballot dumps that go mostly to Biden are explained as obvious fraud (but that is my first time seeing those charts and so like most people I have no “normal” to compare them to); to be clear, I am certain there is fraud just looking for a little more detail to make it more convincing to the general public. So sorry to be the guy with an idea of what you should do because you have already done so much I just don’t know how to do it.
The liberals reply that those large jumps for Biden “are just the absentee ballots being added” with the assumption that Biden got a supermajority of those ballots and so many of the public looking for answers may buy that explanation by the democrats. I think it would be helpful to show how irregular those jumps are. Perhaps it would help if there were charts from other states that show what a normal chart without voter fraud looks like. And the other states could be analyzed so that we could make a statistical statement that proves how irregular those jumps are. Something like this: “in analyzing all other non-voter fraud states no candidate received a jump in ballots of 20:1 (or whatever the ratio is) at anytime except for in NV, MI, WI, PA and GA where voter fraud is suspected.”
What I find a not so strong point it the “they can’t count so fast” argument regarding the spikes.
Millwaukey: here come the Absentee Ballots’s
https://twitter.com/mattsmith_news/status/1323914505638809601?s=20
Here they enter the courthouse, like a count on paper or in a usbstick, I don’t know.
https://twitter.com/MegJonesJS/status/1323917061291204609
They don’t have to count them any more, they are not dragging in boxes of votes?
They add this to the tally and boom you have a spike?
Hi Patrick and Team,
Great work! Can you list out the places and vote counts of the batches of votes that were Biden only (several hundred or thousand votes in a row). What was the quantity of votes and where did it happen?
Thanks for your insights and efforts to ensure fair elections. Please address this discrepancy in the number of ballots sent out versus those received in Pennsylvania. How does that square with these numbers cited in this article? https://apnews.com/article/election-2020-pennsylvania-elections-voting-2020-presidential-elections-b1fe12514c3a736ec33f84e4ce7e4161
Also some people explain that the spikes were just due to uploading of number totals after counting the ballots. How do you respond to this? From the graphs it seems both Trump and Biden had spikes except that Bidens was higher at those ‘injection’ points. How do you determine the Biden that spikes were fraudulent? I assume you have more evidence than you are sharing here but that needs some clarification. Would appreciate some more detailed explanation of the last three graphs. Thanks.
From your linked article:
“A week ahead of the Nov. 3 election, applications in the presidential battleground state of Pennsylvania for mail-in or absentee ballots exceeded 3 million, with Tuesday the last day to request one and legal wrangling creating uncertainty over the deadline to receive them.
State data shows that, of those applications, about 1.9 million, or more than 62%, have been returned to counties.”
So, a week before Nov. 3, 1.9 million ballot *applications* had been returned. Each such (valid) application would result in a ballot being mailed. And some fraction of those ballots would then be returned for counting. In light of this data, getting 2,589,242 mailed ballots returned seems quite odd.
Thanks for clarifying that but here is a different article with different numbers that contradicts what Patrick has in his report. How do we know what the actual official numbers are?https://www.mcall.com/news/elections/mc-nws-elections-mail-boockvar-20201102-6awkgylir5dwxlwpklrclhk6su-story.html
Patrik,
You are probably in contact with Jerome Corsi and Robert Steel already if not you need to asap.
Your findings and Joromes Corsis Supreme Court legal strategie rock.
“Jerome Corsi Supreme Court Disallows Statistical Anomalous States Trump Wins in House” with Robert Steel
https://youtu.be/9UGFFnJuwas
thomascr
They were listening
THE SECRETARY OF STATE AND GEORGIA COUNTIES VIOLATED
THE FOURTEENTH AMENDMENT U.S. CONST. AMEND. XIV, 42
U.S.C. § 1983
DENIAL OF EQUAL PROTECTION
INVALID ENACTMENT OF REGULATIONS AFFECTING
OBSERVATION AND MONITORING OF THE ELECTION
143.
Plaintiffs refer to and incorporate by reference each of the prior
paragraphs of this Complaint as though the same were repeated at length
herein
“The Fourteenth Amendment of the United States Constitution provides
“nor shall any state deprive any person of life, liberty, or property, without
due process of law; nor deny to any person within its jurisdiction the equal
protection of the laws. See also Bush v. Gore, 531 U.S. 98, 104 (2000)(having
once granted the right to vote on equal terms, the State may not, by later
arbitrary and disparate treatment, value one person’s vote over the value of
another’s). Harper v. Virginia Board of Elections, 383 U.S. 663, 665 (1966)
(“Once the franchise is granted to the electorate, lines may not be drawn
which are inconsistent with the Equal Protection Clause of the Fourteenth
Amendment.”). ”
https://defendingtherepublic.org/wp-content/uploads/2020/11/COMPLAINT-CJ-PEARSON-V.-KEMP-11.25.2020.pdf
Yesssssss!!!
Thank you
4. Whereas the Dominion and Edison Research systems exist in the internet of things, and
whereas this makes the network connections between the Dominion, Edison Research and
related network nodes available for scanning,
5. And whereas Edison Research’s primary job is to report the tabulation of the count of the
ballot information as received from the tabulation software, to provide to Decision HQ for
election results,
6. And whereas Spiderfoot and Robtex are industry standard digital forensic tools for evaluation
network security and infrastructure, these tools were used to conduct public security scans of
the aforementioned Dominion and Edison Research systems,
7. A public network scan of Dominionvoting.com on 2020-11-08 revealed the following interrelationships and revealed 13 unencrypted passwords for dominion employees, and 75
hashed passwords available in TOR nodes:
8. The same public scan also showed a direct connection to the group in Belgrade
9. A cursory search on LinkedIn of “dominion voting” on 11/19/2020 confirms the numerous
employees in Serbia:
10. An additional search of Edison Research on 2020-11-08 showed that Edison Research has an
Iranian server seen here:
Inputting the Iranian IP into Robtex confirms the direct connection into the “edisonresearch”
host from the perspective of the Iranian domain also. This means that it is not possible that the
connection was a unidirectional reference
A deeper search of the ownership of Edison Research “edisonresearch.com” shows a connection
to BMA Capital Management, where shareofear.com and bmacapital.com are both connected to
edisonresearch.com via a VPS or Virtual Private Server, as denoted by the “vps” at the start of
the internet name:
Dominionvoting is also dominionvotingsystems.com, of which there are also many more
examples, including access of the network fro
11. BMA Capital Management is known as a company that provides Iran access to capital
markets with direct links publicly discoverable on LinkedIn (found via google on
11/19/2020):
The same Robtex search confirms the Iranian address is tied to the server in the Netherlands,
which correlates to known OSINT of Iranian use of the Netherlands as a remote server (See
Advanced Persistent Threats: APT33 and APT34):m China. The records of China accessing the server
are reliable.
12. A search of the indivisible.org network showed a subdomain which evidences the existence
of scorecard software in use as part of the Indivisible (formerly ACORN) political group for
Obama:
13. Each of the tabulation software companies have their own central reporting “affiliate”.
Edison Research is the affiliate for Dominion
https://www.deepcapture.com/wp-content/uploads/Affadavit-from-M.I.-on-Foreign-Involvement.pdf
20. As seen in included document titled
“AA20-304AIranian_Advanced_Persistent_Threat_Actor_Identified_Obtaining_Voter_Registration_Data
” that was authored by the Cybersecurity & Infrastructure Security Agency (CISA) with a
Product ID of AA20-304A on a specified date of October 30, 2020, CISA and the FBI
reports that Iranian APT teams were seen using ACUTENIX, a website scanning software, to
find vulnerabilities within Election company websites, confirmed to be used by the Iranian
APT teams buy seized cloud storage that I had personally captured and reported to higher
authorities. These scanning behaviors showed that foreign agents of aggressor nations had
access to US voter lists, and had done so recently.
I am making 70 to 60 dollar par hour at home on laptop ,, This is make happy But now i’m Working four hour Dailly and make forty dollar Easily .. This is enough for me to glad my circle of relatives..How ?? I’m making this so u can do it Easily
HERE…… Visit Here
PB how is this crap getting posted? can we take these scum suckers off of here.
Usually there’s a way to flag spam, but I think it needs to be activated.
Hate to break it to you but its because Patrick isn’t very smart. He’s not some tech genius. He has millions of dollars but his website looks and functions like its from 1995. That should tell you something.
hello
hello
hello
Thanks Patrick and team…
Never show your opponent or enemy your hand…keep the info close..some things are not meant to be shared. IF one does share..only share enough to make them sweat BUT NEVER your whole hand. It only gives your opponent..enemy a chance to cover their tracks. My motto..thanks to my good ole dad..TRUST NO ONE. Blessings to you…
Melissa…
Thanks Patrick and team…
Never show your opponent or enemy your hand…keep the info close..some things are not meant to be shared. IF one does share..only share enough to make them sweat BUT NEVER your whole hand. It only gives your opponent..enemy a chance to cover their tracks. There will be a time and place to share it in its entirety. My motto..thanks to my good ole dad..TRUST NO ONE. Blessings to you…
Melissa…
God bless you sir & may the angels forever be in your corner.
COMEON MAN. I CHEATED. Quit lookin around dammitt. s/s joe dunce biden
Thank you so much for your hard work. Thank you for the time and effort put into this. Thank you for standing up for the American people and the integrity of our vote. We are the United States of America, this should have never happened in our country.
Sharon
With respect to the data table that reports PA sent out 1.8 mil ballots; roughly 1.5 mil were returned but Biden captured 2.6 mail-in votes…Is there hard evidence for this claim? Do the election officials certify these numbers? If so, what is their explanation? And given this information why would Biden be certified a winner at all?
Thanks again Patrick and team!
I posted a few days earlier about the possibility of generating ballots for registered 2016/20 non 2016 voters for either party. This would seem to be the cleanest way to cheat. A candidate wins a states electoral vote by popular vote – not by counties won. Suppose the following – Hillory Clinton lost a state by 30,000 votes in 2016 and Biden won by 10,000 in 2020. That’s a difference of 40,000 votes. Suppose this state has 30 counties and 100,000 registered 2016/20 but non-voters in 2016 and all 100,000 registered 2016/20 but non-voters in 2016 had fraudulent mail-in ballots generated for 2020. On average the 40,000 vote difference between loss in 2016 and win in 2020 averages 1333 per county for Biden. All 40,000 could have come from one large county or could have been spread over all 30 depending on the number of registered 2016/20 non-voters per county from 2016. It could be that Trumps numbers in each county mirrored or increased in 2020 vs 2016. Trump could have actually won 29 of these counties in 2020. But if he loses one and the one loss offsets his gains in the other 29 combined he loses the state. The smaller the margin of victory for Trump in each of the 29 counties means a smaller dump necessary in the one Biden county of victory. IF 1000 fraudulent mail-ins were released for 29 counties then 11,000 would have to be released in Biden’s one large (population) county of victory. Spreading the fraud around would seem to be a smart strategy – harder to detect. Now big question number 1 – what if some of the 40,000 registered 2016/20 non-voters in 2016 actually voted in 2020 either walk-in or mail-in. Well duplicates once processed could be mechanically thrown out – in reality I suppose both should be thrown out – the first and the duplicate but if there’s fraud involved the software probably retains one Biden vote. In addition suppose per late 11/3 results Biden was losing – well there just happens to be another 60,000 fraudulent mail-ins ready to be released in one final dump. Big question number 2 – I imagine but do not know t there are machines that can mechanically generate a matching signature based on a sample. So given access to voter registration signatures each of the fraudulent mail-in ballots could be signed with an almost exact registration match signature – this cannot be assumed – signatures must be verified, in fact exact matches could be questioned . Big question 3 – what type of stock and format was used on the fraudulent ballots – this could be a smoking gun – if mail-ins do not match the official stock and format of official mail-ins they must be thrown out. However, if the stock, format and signature match I’m at a loss – the actual VOTER would have to be contacted and willing to testify yes I voted or no I did not. Finally – Big question 4 – does each mail-in have a postmarked envelope 11/3 or earlier – if pre-prepared as stated earlier I imagine they have envelopes but do they have valid postmarks of 11/3 or earlier? This is why all mail-ins without an envelope or postmarked after 11/3 or no postmark at all must be thrown out. In addition postmarks must be validated – I believe the post office has record files of received mailing with process dates separate from the postmark itself – if so this must be verified for any mail-in envelope with postmark of 11/3.
Thank-you!
Patrick,
My son’s name is Patrick, my dad’s name is Patrick, my middle name is Patrick, somehow this makes me an ideal candidate for a response……
Thank you for sharing your brilliant work. It is disappointing, not surprising, that government officials didn’t show for that meeting. The rabbit hole goes deep, and needs to be unearthed.
Sean O.
Great work keep it up
Patrick,
First, THANK YOU for your work on all this, from one liberty-loving American to another. It’s people like you who help the rest of us get through all this with some hope and clarity as to what this fraud actually was and how it was perpetrated. Apparently we can’t count on the mainstream journalists to do so, mostly because there don’t seem to be any left.
Second, while reading through the article, I tried clicking the hyperlinks to what appear to be citations (e.g., “i” or “ii” at the end of key statements/sections. But they don’t jump to anything. Nothing happens. Thought I’d mention it in case there’s something broken and you want to have someone fix it.
Best,
HE
Hi Patrick,
I offer my services to help with the election fraud investigation project. I’m a retired software engineer. I’ve worked with machine and assembly language in developing communications and operating systems. I created a backdoor into a communications system I developed in order to support it long before the Internet was the public entity it is today. If you would like my assistance, email me.
Mark
Thank you so much Patrick for this great service to America. God bless you.
Thank you Patrick for all that you are doing. I fear if this fraud is allowed to stand it will be the end of free and fair elections which will mean the end of liberty and freedom. The whole world is riding on the shoulders of great patriots like yourself.
May the God of the universe, keep you safe and blessed in His hands. Thank you sir for this. Thank you for your courage in helping to save this, the best country on Earth.
Paul Farrell
https://youtu.be/QJ2fTf-wVxQ. Around 3:19 mark the senator starts talking about using BC voting and specifically mentioned Voatz. Way to go Patrick.
I would bet JJ or Saum could get a meeting with the PA Senate to promote
The fraud happened in every state. “It’s every state. Literally every single one. Just to clarify,” he said.
“They didn’t just cheat this election. They needed to cheat it so hard they needed to unplug it at 2am (EST) to catch up,” he added.
This guy shows it was in every state:
https://headlines360.news/2020/11/19/trump-votes-transferred-to-biden-on-election-night/
Thank you for what you are doing for the country. It’s very noble and I realize it can’t be easy. Being a hero isn’t easy, especially making yourself a target of the vindictive sometimes criminally insane leftists. Stay safe.
Patrick; Have you seen the analysis done by Edward Soloman of election rigging in Philadelphia precincts?
https://www.youtube.com/watch?v=KIlI46HdqKg Also his analysis of the programming and algorithms used to switch votes; https://www.youtube.com/watch?v=i1N5bn4TJes
Awesome work Patrick, if I can help in any way, or send some money please let me know. Expose this massive fraud. Thank you – Thank you.
He said the best way we can help financially is to donate to Sidney Powell at her website defendtherepublic.org – Let’s put our money where our mouth is patriots!
Shit my bad, I put the wrong URL. it is
DefendINGtherepublic.org
Los Angeles county hired smartmatic to create a new voting sytem and it was introduced in the 2020 primaries before VBM was made law by newsome. Here is a interesting look at the presidential election: https://results.lavote.net/#year=2020&election=4193
80% of the votes were VBM and the VSAP system is pretty secure but only if you vote in person which only 20% did.
https://votingsystems.cdn.sos.ca.gov/vendors/LAC/vsap2-1/vsap21-funct-reprt.pdf scroll down to page 9 to see the diagram, most of the hardware have PKI to secure the platform to the tally except VBM, which is scanned by hand. CA was most likely the test ground for election fraud as most counties use dominian.
https://votingsystems.cdn.sos.ca.gov/oversight/county-vsys/vot-tech-by-counties-2020-11.pdf
Just wondering about the data source for these graphs. Are you using the JSON files that were supposedly produced by Edison Research and downloaded from an NYT website? Or do you have some other source of election-return data? It is not clear how that Edison JSON data was compiled, or even whether it really was produced by Edison.
Patrick, I am very proud to be a fellow countryman of yours. Great work and thank you! The presidential election is, of course, front and center to save the Republic. And you are on it, my man. When this smoke clears and there is time for you and fellow Patriots to look into the full scope of the fraud in all 50 states, I hope that there is an opportunity to look at North Carolina in detail. While Trump nominally won the state, I do not believe his margin of victory (it should have been WAY higher), but, as importantly, I really do not believe the margins for the Governor, US Senator, Attorney General and perhaps several races for the Congress and the General Assembly from both parties. This looks and smells like a seriously rigged election but one done with a strategic eye to not arouse too much suspicion or a forensic audit, which is necessary in my view. NC also uses ES&S machines for vote tabulation. All help is appreciated more than you can ever know!
LOOK FELLOW PATRIOTS TWITTER IS TRYING TO SENAOR THIS https://mobile.twitter.com/PostRoz/status/1332467663076012034
Patrick,
Since I watch Quite Frankly’s livestream most evenings, I caught your interview. You always have little tidbits you’ve withheld previously! Per your suggestion, I donated to Sidney Powell.
RedPill78 (a friend of Frank’s) had over 250,000 youtube subscribers (including me) before he was banned. He now livestreams on several platforms so I hope he invites you on his show. You’d like him — he used to broadcast with his cat on his shoulder (she died a short while ago). https://redpill78news.com/
Your graphic about Pennsylvania’s official vote count is fraudulent. And I’m a PA resident who voted for Pres. Trump.
The vote counts shown in the table are correct for the 2020 General Election. The statement in the caption “Pennsylvania reported having mailed out 1,823,148 ballots, of which 1,462,302 were returned” is correct, but it refers to the 2020 *Primary* Election. You can confirm (as I have) that the numbers 1,823,148 and 1,462,302 are correct for the 2020 *Primary* Election dataset, which is available at https://data.pa.gov/Government-Efficiency-Citizen-Engagement/2020-Primary-Election-Mail-Ballot-Requests-Departm/853w-ecfz
You should remove the graphic from your page, or, even better, leave it and explain its fraudulent nature.
He won’t because he is a bad faith, dishonest fraud.
Will Americans ever know the truth regarding 2016 election fix and foreign government interference with the scam?
yea I really want to know who stopped shillary from stealing the 2016 election.
Russia…
Patrick, could you reach Sidney or her web guru and ask them to get defendingtherepublic.org Brave browser verified. There are thousands if not 10’s of thousands of Brave users that will donate their BAT earnings.
For all. Brave.com is a super fast and very secure browser that does not send data to google, AWS and the like. You can choose weather you want adds on your pages or not and if you do choose to see add YOU are paid a good portion of the add revenue. You can transfer and exchange your payment for US $, as I have done once or twice, or you can support web sites, twitter users by “Tipping” a portion of your monthly earnings.
Patrick has done much more than just fight for our elections. He started https://www.mediciventures.com and put together a group of Block Chain companies that could transform our government and financial functions almost over night. He also backed an idea by Bruce Fenton for an open source Block Chain that any one can use to build a business, service or any number of other things. Ravencoin.org has an outstanding set of functions and features that allow for millions of use cases. You can find a partial list of some of the businesses taking advantage https://raven.wiki/w/Ravencoin_Wiki
Ultimately all revolutions fail without a viable alternative to fill the void ready to go. Patrick has given us a path and the tools to create the FREE country we were lead to believe we have.
Pretty sure it’s your mouth that should be glued shut.
Just wondering about the PA figures regarding the total number of mail-in ballots sent out. USA Today and Snopes are saying that the number was taken from the number of primary election ballots sent out. Do you have info on this to help clarify?
Praying for truth in the election results ASAP. God bless you, and Sidney Powell.
The graphic is fraudulent. The numbers in the table are from the PA 2020 General Election. The numbers in the caption are indeed from the PA 2020 Primary Election. I have personally verified this, and you can too, if you spend a few minutes with the dataset at
https://data.pa.gov/Government-Efficiency-Citizen-Engagement/2020-Primary-Election-Mail-Ballot-Requests-Departm/853w-ecfz
Got it. Tracked it down and could not verify. Removed it.
Will add more about Pennsylvania though.
Decent of you to remove the false info.
“Could not verify” is an interesting way to say that it was complete horseshit. You in fact are able to verify that it was 100% wrong information that you happily spread around and are now backing off in the meekest possible way.
If the fraud was so obvious why is so much of the “proof” from you and people like Sydney Powell an outright lie?
* Lying about the number of registered voters in PA
* Lying that the Georgia state certification of the Dominion equipment wasn’t dated when in fact is that it was but the date was cropped out for the lawsuit?
* The Michigan suit claims there was fraud in Edison County Michigan, which literally doesn’t exist
I don’t expect you to answer this because you are obviously a fraud and you have found a large enough following of complete rubes to believe any of the trash you put up. I just want to say it is really sad to watch someone who used to be reasonably respected lose his mind and embarrass himself in such a way at the end of his career.
Bill Barr just announced that the DOJ could not find any evidence of election fraud.
The same Bill Barr that said Epstein killed himself…
Nothing to see here just keep moving
3 Star General says you, MJ, are guilty of treason. Why don’t you let the adult in the room talk.
https://youtu.be/i1GSmgdt-Ik?t=1609
And this might be the SMACK DOWN of the year. PB you need this Phd. on your team.
https://youtu.be/X0-vyw9qbdw?t=23233
HAPPY BIRTHDAY PATRICK !
What time were you born? I’ll ask my favorite youtube astrologer to see what 2021 has in store for you, especially concerning your health and personal safety.
Corruption fighters on both sides:
“It is past time to put an end to the secrecy that allows drug cartels, human traffickers, arms dealers, terrorists and kleptocrats to exploit the United States’ banking system in order to carry out anti-American activities. That’s why I’m pleased to know that this year’s defense funding bill will include the ILLICIT CASH Act – legislation I introduced to combat money laundering and terrorist financing,” said Sen. Warner.
https://www.warner.senate.gov/public/index.cfm/2020/11/senate-intel-vice-chairman-warner-on-inclusion-of-his-bipartisan-national-security-legislation-in-annual-defense-funding-bill
This is a response to the comment above since I couldn’t respond to that one. Don’t you find it odd that you can’t answer any of my questions even though they are very simple, instead you resort to name calling? Not that I really care what Michael Flynn has to say since he is an admitted liar, but what treason have I committed by pointing out that Sydney Powell is at best an extremely sloppy lawyer?
That was not Lt. General Flynn it was 3 STAR General Thomas McInerney saying whoever is trying to hide this is committing treason.
The 3 things you listed as reasons for saying all this is BS are the weakest arguments you could make. Anyone with a simple knowledge of data could see all the issues.
How about defending the vote spikes very evident in the raw data?
How about defending 3200 Trump votes out of 570K?
How about defending the packets transferring between Dominion machines and foreign servers?
This list could go on and on….
I didn’t vote for Trump and think he should be in prison along with the Bidens, Clintons, Bushes, Obamas and anyone who help commit this treason.
BTW this story was first reported back in 2015, where the hell have you been?
“Dennis Montgomery, the CIA / DoD contractor-turned-whistleblower who designed and built THE HAMMER foreign surveillance system and its exploit known as SCORECARD, provided sworn testimony to the FBI and the DOJ in 2015 about THE HAMMER, SCORECARD, and SCORECARD’s capability to hack into election systems from Dominion, Smartmatic, and other .”
https://theamericanreport.org/2020/11/19/release-the-kraken-hammer-scorecard-whistleblower-montgomery-gave-sworn-testimony-to-fbi-and-doj-about-scorecard-dominion-smartmatic-in-2015/
Sad when people you trust are 2 faced liars.
You will win this fight.
All the nit wits that use Technology
(WIFI.LTE.3G.5G.satellite.electric)to hack devices and takeover apple fonts (using shortcuts)in all apps IS A TECH EMPLOYEE. mee thinks.
Know when you are attacked with condescending remarks you are on track-
people who are fighting for truth.
You are important. Your life is important.
I am important. We all are important.
I hope the sorry con artist that used you calling
You friend will someday have to puke up truth.
Funny location services is everywhere except where i am and i have to see queer ads.
(Ad based tracking for the hacker)
Thank you for dropping the wall of silence.
May God carry you through this bleak time and throw you into the sunshine – the future.
No matter what the outcome- we are left looking at an evil monster that dropped its pants. rather then talk about trump, we need to talk about America 2050. Folks America has failed. When Tyranny wins and people sleep, we are already lost. The question is are we going to just go along with this globalist takeover, or can we stand up and take this country back. I would rather unplug my computer, and live outdoors free, then live in a commune.
Also, to all: we don’t have a large burden of proof. The graphs are enough preponderance of evidence to show that the election has been tampered with. All we have to prove is that the average person would agree this election stinks. We don’t have to prove beyond a reasonable doubt. That is why , if we loose this, we will never see Americans in office again. The Democrats are already erasing our memory from social media. Anyone had all their subscriptions deleted from YouTube yet? I did. Too many Conservatives views in one account. Someone deleted all of them!!! An I am nobody!!! Imagine what they will do, once they have the power back!!
Battle stations!! we need to convince the other half that Globalism and what they are painting is a freaking communist’s country!!!
Twilight zone: How to Serve Man, was given to humans from the aliens first contact. The Democrat AMerica 2050 is how to serve man! Its a cook book!!
Wake Up!!!
Hi, Patrick. I just watched your interview with Dr. Dave on Operation Freedom regarding Dominion/Smartmatic election systems and election fraud. I live in Montgomery County, NW of Philadelphia. I understand there was rampant fraud in my county as well, although I didn’t witness any voter intimidation. By the way, I was handed a Sharpie, which troubled me, but the scanner accepted my ballot…or so it said. I wonder now if my vote was redeployed as I did not vote for Biden.
I’ve been following a few data guys on public Twitter regarding all things coronavirus. Some identify themselves and some have avatars (I gather they want to keep their jobs and their families safe).
One in particular, @gummibear737 has been following the absentee ballot data in Pennsylvania. I don’t know his qualifications or background.
Would really appreciate it if you would look over his data. While it’s not hard data (like Matt Braynard’s work for Project Amistad), it certainly suggests fraud on a massive scale.
https://twitter.com/gummibear737/status/1332671791433707522
Thanks!
Mr. Patrick Byrne,
You simply need to set up a secure Web site for each battle ground state where people who voted for Trump can submit an affidavit that they voted for Trump. The count will tell the true story.
Of course you would need a scheme to avoid jerks who would flood the site with false affidavits.
Patrick,
I just got banned from the Daily Mail for posting ‘educational’ comments about the election. Good time to take a break from the internet, relax and listen to the radio while I cooked dinner. Gosh, that guy Kathleen Wells is interviewing sounds familiar… I pictured motorists stuck in post-holiday traffic on the freeway hearing you and this information for the first time. No escape!
Patrick, peak at Snopes search “chicago o’hare driver license” to see 1/1/20 to 6/30/20 confiscation of 19,888 quality counterfeit U.S. college-aged driver’s licenses. Imagine U.S. groups sending individual’s photos and ordering IDs (even multiple quantities) for each photo. Imagine fake IDs getting through at the five targeted cities. IDs get distributed to individuals for registering and voting each ID. Absent facial recognition technology to compare photos, weakness in process of building/audit voter roles.
Need this guy on the team:
The New York Times published a glowing report on Dr. Navid Keshavarz-Nia way back in September writing, “Navid Keshavarz-Nia, those who worked with him said, ‘was always the smartest person in the room.’”In his statement to Sidney Powell, Dr. Keshavarz-Nia concludes that the election data IN ALL BATTLEGROUND STATES were altered resulting in hundreds of thousands of Trump votes transferred to Joe Biden! (GP)
https://gellerreport.com/2020/11/nyt-endorsed-leading-cyber-crimes-expert-concludes-election-2020-data-were-altered-in-battleground-states.html/
It is rumored that China forged votes, videos and dialogues flow out
As the US election was affected by the epidemic, more than 120 million blank ballots were mailed in advance. According to a source, an underground factory in Guangdong, China, which usually specializes in “forging invoices and falsifying accounts,” has forged a large number of blank U.S. ballots since July with a monthly output of 500,000.
Judging from the screenshots of the conversation, the boss not only said, ” We have the original version of this version, “We have ordered it before . ” There is still a lot of this in inventory. And because the ballots are different in each state in the United States, the underground factory can provide the original model files of “Mississippi, Florida, North Carolina”, and emphasize that this is provided by the “previous customer”, and there are other states that can also be used for voting , Not only these 3 states.
It is worth noting that the boss of the underground factory actually stated that the metal patterns and anti-counterfeiting of the real ballots cannot be forged yet, but previously unknown people have ordered a large number of them, and the boss also said, “The amount is not a problem, the main thing is your money. In place, that amount is not a problem.”
https://www.cmmedia.com.tw/home/articles/24456
Regarding the fact that China forged a large number of blank ballots in this U.S. election, after a citizen journalist’s introduction, the third generation of the CCP Red, named Yi Qiwei, confirmed that this happened, and pointed out that a large number of fake driver’s licenses and fakes from China were seized throughout the United States this year. The certificate is also related to this incident. Yi Qiwei quoted a report from “Voice of America” and pointed out that as of August 10, US law enforcement authorities had intercepted 54,718 fake identity documents.
Info in there worth looking in to…
Patrick,
I am in cyber security and greatly appreciate what you have done and the data you shared. What I am still trying to piece together is the actual forensic connection between the setup described in affidavit from the Kraken and the footprint of the bad actors. I apologize if I missed it.
But you clearly show how someone (foreign bad actors) could manipulate the election (the voting spikes) but is there actual audit log information showing who did it? What credentials were used? Can the sequence of actions be shown definitively between the how and who?
I have no doubt this happened. Just looking for the irrefutable evidence. I am afraid a judge would say this is all very damning but it doesn’t actually show someone did it…it only shows they could.
Thanks again and God Bless!
Thank you Patrick. The graphs show things so clearly. America appreciates your work and your bravery for publishing it. If we can help at all in SC feel free to reach out. The math doesn’t lie.
You might be able to get a copy of the source code:
Dominion is required to hold source code and all its variations in an escrow vault with an agent
https://gellerreport.com/2020/11/dominion-software-source-code.html/
Keep being the American Patriot that you are!! This needs spread around the world! Thank you so much.
Sorry I can’t see in the hundreds of comments if the below issues were already addressed, but these are my comments on this paper:
1/ Re “[i] By way of example”, 2nd bullet:
First, It’s unclear what servers are being referenced in this comment. Are you referring to a “summation server” that all tabulation servers report into? The article seems to imply you are talking about tabulation servers. To me, it seems like physical servers would be far easier for local precinct folks to set up and tear down. Regardless, nobody has said anything much about system architecture or implementation (especially state-by-state). QSnatch would only apply to virtual servers running on the vulnerable storage system. Who knows what storage system any state’s servers were running on?
2/ Re: same bullet point:
The reference to audit trail is a completely separate issue which refers largely to lack of a secure system architecture. There should be a Risk Management Plan, a set of ISSP’s in accordance with NIST guidance, and secure baseline’s for all devices.
The tabulation servers should be locked down in accordance with designated STIGS, including establishment of event log levels and forwarding of all events back to the organization’s (state.gov) central event logging system. Audit logging is just one security element of hundreds.
As another example of VERY BAD security implementation, Bowen Xiao reported that GA servers were reportedly configured to permit split tunneling via a wireless card. If true this is absolutely rock bottom poor security.
I suspect, based on what little we know, that a review voting machine IT policy, process and procedure, and device baselines would reveal *hundreds* of security defects.
To me, this pits the lie to what the idiot Krebs said about election security. To real security professional would make the claim that dope made.
Re: [ii] (NYT reporting)
Supply chain risk is among the most difficult IT risks to manage. This risk is usually mitigated through extensive V&V testing which is thoroughly documented and submitted to records management. This risk was largely accepted when the system was procured and this paper is over dramatizing it relative to risks created by lack of a secure overall implementation. This in turn diminishes the impact of your report. A simple statement that V&V testing was not just inadequate but incompetent left the states open to realizing the risk. Again, though, this is just a prt of secure operation of an IT system.
I think you have three issues:
1/ System design issues noted at the very top.
2/ Very very very bad over system security, whixh in mind rises to the level of complete incompetence to run a secure IT system.
3/ Statistical evidence fraud occurred.
Apologies for all the grammar/spelling issue. All thumbs on the phone here…
One correction. I should have said virtual servers running on a virtual machine arop the storage system. I’m not familiar with the storage system and/or VM mentioned and it was unclear to me what exactly was vulnerable to Qsnatch. The VM seems more likely that the underlying storage system. This should be clarified. Sorry for any confusion on that point.
The question is. how do you get the people of America, the courts, and the politicians to admit that this is a farce? You can’t tell me that the average American can’t say that yes something is wrong when election officials will not let the votes be observed. Find a way to get the word out. Thank you for the work you are doing.
Votes were observed by watchers from both parties. This is one of the dumbest and most easily disproven pieces of “evidence” that there was fraud. Grow up and get your news from somewhere other than OAN and the website of an old man who has lost his mind.
We saw in Philadelphia the video evidence of Republican poll workers being locked outside of the main counting room and democrats taping poster board to the windows so they could count ballots without oversight you putz . . . You couldn’t see it because your head was too far up your a$$. You are part of the problem with your insanely stupid comments.
“observing” is one of the dumbest and most easily disproven pieces of propaganda from all the bureaucrats of electoral fraud….
In many cases “observers” were kept too far away to actually “observe” anything specific about the ballots…
In a variety of other cases “observers” were told to go home because the vote processing was (supposedly) to be suspended for the night, but then Democraps went right on “counting” whatever they pleased.
So take your Mr. Anonymous “trust the observers” lie and put it back where the sun doesn’t shine.
Some good information on Scytl problems in other countries:
https://www.republik.ch/2019/01/31/das-heikle-geschaeft-mit-der-demokratie
https://www.spiegel.de/netzwelt/netzpolitik/spd-online-abstimmung-ccc-warnt-vor-umstrittenem-wahlverfahren-a-1291616.html
https://www.spiegel.de/netzwelt/netzpolitik/schweiz-sicherheitsluecke-in-wahl-software-entdeckt-a-1257563.html
“As the Republik-Magazin recently showed, Scytl is not even able to correctly carry out so-called e-counting, that is, to count paper slips with electronic support,” says Hernâni Marques, spokesman and board member of the Swiss CCC, DER SPIEGEL. In the European elections in May, numerous votes went to right instead of left parties in Spain. “When it comes to online voting, Scytl has failed completely, showing that it has no idea of the underlying mechanisms,” said Marques.
I fear that we are running put of time and the will to intervene in the courts. Even SCOTUS.
BUT can we stop these machines be forbidden from use in future elections until they are audited? That includes an independent verification and validation of their source code that would address back doors and cyber security in general.
I work on digital safety systems in Nuclear Power plants and all of that applies to the systems we provide.
getting posting errors trying different browser.
Some good information on Scytl problems in other countries:
https://www.republik.ch/2019/01/31/das-heikle-geschaeft-mit-der-demokratie
https://www.spiegel.de/netzwelt/netzpolitik/spd-online-abstimmung-ccc-warnt-vor-umstrittenem-wahlverfahren-a-1291616.html
https://www.spiegel.de/netzwelt/netzpolitik/schweiz-sicherheitsluecke-in-wahl-software-entdeckt-a-1257563.html
“As the Republik-Magazin recently showed, Scytl is not even able to correctly carry out so-called e-counting, that is, to count paper slips with electronic support,” says Hernâni Marques, spokesman and board member of the Swiss CCC, DER SPIEGEL. In the European elections in May, numerous votes went to right instead of left parties in Spain. “When it comes to online voting, Scytl has failed completely, showing that it has no idea of the underlying mechanisms,” said Marques.
hiu
hi
Just heard you on Glenn Becks program this afternoon on the way to lunch. Great job of presenting your case. I immediately pulled over and saved your web url. The amount of evidence you present is staggering. Hopefully it gets into the hands of people who are able to do something with it.
Godspeed man, you’re doing great work.
Patrick
https://www.businessinsider.com/ag-barr-confirms-lack-of-widespread-fraud-in-election-2020-12
Betrail???
What the heck??
And where is Durham???
thomascr
and…
PATRICK
Why is Mark Zuckerberg “DONATING??” 400 millions of USDs to help riggggg the ELECTION??? …
LIBRA
simply disgusting that a millennial new rich couple can pull this off to make more billions for them selves for the sake of fb “free press and a fake democracy” …
I guess I need to throw up
thomascr
The Left is a Lie.
Need incrementing evidence and not mathematical mumbo jumbo to change the minds of the lemmings. We could ask Joe, I’m sure he would be proud to explain how and who did the rigging for him? Actually, he was probably telling Hunter all about it when they broke his foot to shut him up? They need to keep a tight leash on that guy before he blows it for them…does the White House have a basement?
The investigation centers on Staple Street Capital, which acquired Dominion Voting Systems in 2018.
Dominion Voting Systems operates voting machines in 28 states and has been accused by President Trump and his supporters of being involved in deleting millions of votes for Trump in addition to switching votes to Biden on election night.
Firm That Owns Dominion Voting Systems Received $400 Million From Swiss Bank Account Funded By Communist Chinese Gov & Companies Before Election
“On Oct 8, 2020, Staple Street Capital filed SEC Form D offerings and sales amount of $400,000,000 with the Sales Compensation Recipient identified as UBS Securities,” states the investigation, which also notes that another payment of $200,000,000 was received in December 2014.
“UBS Securities is a swiss investment bank which owns 24.99% of UBS Securities Co LTD, a Chinese Investment Bank. The remaining 75% of UBS Securities CO LTD is owned by the Chinese government,” states the report.
https://humansarefree.com/2020/12/firm-that-owns-dominion-voting-systems-received-400-million-from-swiss-bank-account-funded-by-communist-chinese-gov-companies-before-election.html
I have read a lot of SEC filings since first finding deepcapture over 10 years ago but never have I seen a company with just 4 filings in 6 years.
https://www.sec.gov/cgi-bin/browse-edgar?company=Staple+Street+Capital&match=&filenum=&State=&Country=&SIC=&myowner=exclude&action=getcompany
Great interview with Glenn Beck. I will share your information with all who are willing to listen.
The data is phenomenal; however, I am afraid without a critical analysis and well-written synopsis, most of these data will go right over the head of almost all people. PLEASE, invest in some time breaking down the major points of irregularities (standard practice vs what happened here), illegalities (what federal and state laws were broken), and statistical impossibilities (calculate the p-values that show the 1 in a billion scenarios that “happened”).
Thank you! You are a scholar and a gentleman!
Why were Robert Mueller,John Brennan, James Clapper, and the CIA unmasking and hacking so many voters in GA, PA, NV, MI, OH, FL, TX, NC, AZ, and so many more?
Leverage and Control of our elections!
GE
Target: Voters
GA (451,427 voters)
PA (87,430 voters)
OH (479,456 voters)
MI (547,545 voters)
AZ (492,075 voters)
NV (87,406 voters)
FL (304,533 voters)
TX (2,077,096 voters)
NC (399,902 voters)
CA (2,022,144 voters)
Limited data provided here due to sensitive information. Full dataset was provided to the FBI and DOJ under immunity agreements.
amg
US voting machine manufactures and their employees were hacked in illegal FBI/NSA/CIA domestic surveillance programs we worked in from 2003-2016. The proof was provided to the DOJ and FBI by a whistle blower in 2005, 2008, 2010, 2012, and 2015. The data was provided to FBI Director James Comey’s general counsel James Baker on 08/19/2015 and 12/03/2015.
https://www.blxware.org
“Trump Blasts Durham for Not Finishing Probe Before Election”
Electoral disasters plus totally inadequate “investigations” by the federal govt entities….. Just another reminder that Q/Qanon was 3+ years of preposterous bull droppings. Despite the “Q” claims that “we have it all” and “enjoy the show” etc. in the end NOTHING was done to protect the Trump presidency, electoral integrity, and Trump’s re-election.
The Q/Qanon stuff is just a sideshow but it consumed tons of time and energy from conservatives who should have had much better things to do.
I remember well how “Q” boasted that “Trump surrounds himself with Generals” because that was supposed to indicate that the Trump admin. was some kind of elaborate 12-D military intel operation to save America. Well of course, as we know, Mattis-Kelly-McMaster were all great anti-Trump disasters…. while General Mike Flynn despite his good intentions was back-stabbed right out of the administration and into a 4-year legal catastrophe that had to be ended by a pardon.
So much for the efficacy of “Q” and “Trump’s Generals” and every other piece of b.s. spread by the moronic “Qanon” crowd for the past 3+ years. Anyone who still takes “Q” seriously is an utter moron. Well that was evident 3+ years ago….
“Trump Blasts Durham for Not Finishing Probe Before Election”
“…Trump lamented that findings from Durham’s investigation into potential FBI malfeasance in its probe of Russian meddling in the 2016 political cycle didn’t surface before the most recent election last month, effectively altering the course of the race.”
“”We caught them all,” Trump said from the White House Diplomatic Room. “We’re still waiting for a report from a man named Durham who I’ve never spoken to and never met. They can go after me before the election as much as they want, but unfortunately Mr. Durham didn’t want to go after these people . . . before the election, so who knows if he’ll ever even do a report.””
https://www.newsmax.com/us/election-fraud-john-durham-investigation-special-counsel/2020/12/02/id/999766/?ns_mail_uid=02e7e076-ed9b-4a1d-9672-a4525ae8b5dc&ns_mail_job=DM169366_12022020&s=acs&dkt_nbr=010504zomuo6
Hilarious!! Voter fraud?? Why not just present the evidence in maybe 1 of the 30some cases Trump filed? Cuz there is none sheeple! It’s not a conspiracy. He lost. Now he’s rolling you, his supporters, for all he can get out of you by alleging fraud only to have you get pissed and contribute to his “fight”. Read- pockets. P.T. Barnum would be in awe of the con job he is doing on you and you eat it up! Gluttons for more! Thank you sir may I have another! My God. Wake the hell up! He is a farce. Always has been.
You sir BETTER WAKE UP!!! Biden and many, many others have you and many others totally blinded!!!
I plotted the fraud frozen in the final fractions of red:blue :: potus:senus:repus votes across localities for states: PA, GA, CO, SC, VA, WV, and for Wayne and Oakland Counties in WI. Only the SC plot appeared fair.
Plots and open source here: bit.ly/3oh0DEN Gab here: bit.ly/37v9MTx
Hi Patrick,
I just read some posts Bev Harris tweeted and they got me thinking.
I would like to draw your attention to the following:
https://informeddelivery.usps.com/box/pages/intro/start.action
For some time now the USPS photographs ALL mail pieces, and now uses that ability to send you photos of the mail your are to receive the next day. Proven in the link above, the link proves the image archive.
Fortunately I had not yet emptied my office garbage and found my unopened mail ballot (I voted in person). Interestingly, there is “******-01E” on the ballot (and ballot has that as a 2D barcode) and on the outside of the mail piece. I know ****** is an ID associated with my city. However I am not clear on the last 3 characters. It would be great to see a neighbors mail piece to compare, but unlikely to happen. Using letters and numbers gives a total of 46656 possible combinations (enough for all voters in my city) and thus could be my unique ID, dunno. But if it is, then the post office photo would contain everything needed to match my ballot to my name and physical address as that sequence is also on the outside of the mailer.
Which always begs the question, who has access to all those photos?
There are many other dot matrix printed “notations” on the outside of the mail piece as well. Not clear what they are.
The above “service” of the USPS came to my attention via a story of thieves using it. Basically the post office does not check the service requests so anybody can sign up for anybody else’s address. Then they watch the emails for something of value and then go steal it …
It would be interesting to harvest ALL USPS ballot photos and see what one finds …. The USPS clearly has a database of ALL OF THEM …. The Gov watches us with it, only seems fitting that in this case we use it to take a look at them. On my mail piece there is a huge obviously unique barcode for me that would allow this database to be processed automagically.
The markings on my Ballot mail piece are sufficient to match the mail coming to me, and my mailing it back. The address label “to” me appears on the back side of the return envelope. This then provides even more information, such as were ballots returned and the voter still allowed to vote in person (match to polling location)?
Charles
Charles, you are onto something! And a side note, how interesting is it that up until election day all we heard from the Left and the media was that the head of the USPS was a corrupt Trump loyalist? And since the election, not a peep. Go figure.
Thank you for proving no fraud. Blue mirage in the states that were able to count mail-in and absentee ballots early(your example Arizona 14 days prior to election day), and red mirage in the states where mail-in and absentee ballot could not be counted until election day(Michigan, Wisconsin, Pennsylvania, Georgia…). This is exactly what was expected to happen, and the response is true to form as well.
Now, take Arizona and assume they weren’t able to count early votes until Election Day. It would look like the other charts you have. Or, do it the other way. Assume Wisconsin or Pennsylvania was able to count early votes before Election Day. They would look like the Arizona
All that the charts show is when the early vote tabulations were entered into the system, predictable and verifiable.
In fact, I’m wrong; you did prove fraud on the Republican side. Republican led State Congresses in Wisconsin and Pennsylvania for example would not allow election officials to count early voting until the day of the election, giving Trump the appearance he wanted to further his election fraud agenda.
Wouldn’t you think PRESIDENT Trump, with the whole of the government (FBI, DOJ, and other agencies) at his disposal would have uncovered actual election fraud plots before Election Day? All Trump was and is doing is using NAZI propaganda tactics with his base, and it is sad that so many people have bought it. I’ll share a quote “If you tell a lie big enough and keep repeating it, people will eventually come to believe it.” This is known as the Illusory Truth Effect. Who is the quote from? Joseph Goebbels, minister of propaganda for the Nazis. Trump has told the same “fraud” lies over and over and over again, so people now believe it to be true no matter what comes out to show otherwise.
Open your minds to the actual truth. CISA, FBI, DOJ and others have ALL said it. This was a secure election with no wide spread fraud.
Nothing to see here…. all laws followed to the letter at all times….
https://youtu.be/x-7E-71Av0k
I’m sure a PR person at Dominian was directed to write this. Which of these claims can you refute?
Dominion Voting Systems Menu
Return to Election 2020: Setting the Record Straight
November 26, 2020
STATEMENT FROM DOMINION ON SIDNEY POWELL’S CHARGES
While Dominion Voting Systems is not named as a defendant, on Wednesday, November 25, 2020, Sidney Powell released what appears to be a very rough draft of a lawsuit against the Republican governor and secretary of state of Georgia alleging a bizarre election fraud conspiracy that—were it possible—would necessarily require the collaboration of thousands of participants, including state officeholders, bipartisan local elections officials, thousands of volunteer Election Day poll watchers in thousands of locations across the state of Georgia, federal and state government technology testing agencies, private elections service companies, and independent third-party auditors. This quite simply did not occur.
Dominion Voting Systems is the gold standard for transparent and accountable voting equipment. The allegations included in the draft complaint are baseless, senseless, physically impossible, and unsupported by any evidence whatsoever. We stand with the state and local elected officials and bipartisan election volunteers that this suit maliciously maligns.
In Powell’s error-filled document, she repeats a number of baseless allegations about Dominion Voting Systems, which she has made in public since Election Day.
The allegations about DVS most relevant to the election outcome in Georgia are that votes tallied on a Dominion vote tabulator were somehow manipulated on a statewide basis to elevate the count in favor of the Democratic presidential candidate. It is important to understand that this is not possible—not on a machine-by-machine basis, not by alleged hacking, not by manipulating software, and not by imagined ways of “sending” votes to overseas locations. But even if it were possible, it would have been discovered in the statewide handcount of votes.
Dominion’s systems are secure as certified by the U.S. Election Assistance Commission (EAC). In fact, all voting systems must provide assurance that they work accurately and reliably as intended under federal U.S. EAC and state certification and testing requirements. Further, Dominion source code is verified and secure. Third-party test labs chosen by the bipartisan U.S. EAC and accredited by the National Institute of Standards and Technology (NIST) perform complete source code reviews on every tabulation system that is federally certified in the U.S.
Every vote from a Dominion device in Georgia is documented on an auditable paper trail and creates a verifiable paper ballot available for hand-counting. In fact, the Georgia handcounts, independent audits, and machine tests have all repeatedly affirmed that the machine counts were accurate.
In addition, Powell makes a number of allegations that go beyond Dominion’s role in Georgia’s elections—which is only to provide the ballot tabulation systems. For the record, again, Dominion does not develop voter-registration systems, poll-books, signature verification software, or provide vote-by-mail printing. These parts of the voting process are instead supported by other companies and controlled by the state and local officials who run elections in hundreds of thousands of voting places across the country.
These assertions in the Powell filing are non-sensical and unsupported by any presentation of evidence. However, to respond to some of her specific assertions about Dominion:
Dominion was not “founded by oligarchs and dictators.” It was founded in Toronto, Canada, and it is now a proud nonpartisan American company. Dominion has attested to its ownership—under penalty of perjury—to local, state, and federal agencies, including the Committee on Foreign Investment in the United States, which includes all U.S. national security agencies.
Dominion is not, and never has been, owned by Smartmatic. Neither has Smartmatic ever been a subsidiary of Dominion, as the complaint asserts. Dominion is an entirely separate company—they do not collaborate in any way and have no affiliate relationships or financial ties. Dominion does not use Smartmatic. These are all facts verifiable in the public record as well as in regulatory and legal filings.
Dominion has no ties to the Venezuelan government, nor any other foreign government, including China and Iran. Dominion has never participated in any elections in Venezuela and has no connection or relationship with the now deceased former Venezuelan dictator Hugo Chavez. Other companies have serviced elections in Venezuela, but Dominion is not one of them.
Dominion does not have operations in Germany including an “Office of the General Counsel.”
Dominion Voting Systems are in fact auditable—and are audited and tested regularly by multiple government agencies and independent third parties. All electronic devices used in the U.S. must be designed to be audited.
Dominion’s system does in fact include a paper ballot backup to verify results. In fact, thousands of elections officials in Georgia just completed the largest vote recount in American history using the paper ballots produced by Dominion devices.
Dominion’s system cannot be manipulated by a technician in the way Powell alleges. This has been confirmed by the government agencies that have certified Dominion equipment.
Despite repeated counts and audits, there is no evidence of any kind that any voting system deleted, lost, or changed votes in Georgia, or in any of the other 28 states that use Dominion devices. Certifications and audits have instead shown the accuracy, transparency, and reliability of Dominion’s systems.
The federal government agency that oversees U.S. election security verified that there is no evidence that this election was in any way compromised. In fact, they have called it the most secure election in American history.
Servers that run Dominion software are located in local election offices, and data never leaves the control of local election officials.
There were no “glitches” with Dominion’s voting systems, and no unauthorized or last-minute software updates occurred.
There were no “data breaches” of Dominion software by anyone, let alone rogue foreign actors.
Human errors did occur in some counties but were resolved quickly by county officials before the canvass process.
Votes are not processed outside the United States. Votes are counted and reported by county and state election officials—not by Dominion, or any other election technology company.
Election safeguards—from testing and certification of voting systems to canvassing and auditing—prevent malicious actors from tampering with results.
Sidney Powell’s wild and reckless allegations are not only demonstrably false, they have led to stalking, harassment, and death threats to Dominion employees. This criminal activity has been duly reported to the appropriate law enforcement agencies, and we intend to hold Ms. Powell, and those aiding and abetting her fraudulent actions, accountable for any harm that may occur as a result.
Return to Election 2020: Setting the Record Straight
DVS Logo – HighRes – SVG
Founded in 2003, Dominion Voting Systems is a leading industry supplier of election technology across the U.S., Canada and globally.
PRODUCTS
EMS ENGINE
Democracy Suite®
IN-PERSON AND ACCESSIBLE VOTING
ImageCast® X
CENTRAL TABULATION
ImageCast® Central
COMBINATION VOTING AND TABULATION
ImageCast® Precinct
ImageCast® Evolution
Optional Solutions
ABOUT
Dominion Difference
Dominion Secure
Careers
INFO
Customer Support
1-866-654-VOTE (8683)
Contact Us
U.S.: Denver, CO
CANADA: Toronto, ON
Privacy Policy
Terms of Use
Site Map
Copyright © 2020 Dominion Voting Systems Corp.
All Rights Reserved.
Dominion Voting Systems
HOME
ABOUT
PRODUCTS
SUPPORT
SECURITY
CAREERS
CONTACT
How can I share this article on other sites such as facebook. I’d like to help get the truth out.
Hey Patrick… Hollywood needs to make a movie about your life. I wonder who will play your part?
Tom Hanks
Brad Pitt
And your co-star should be Margot Robbie
Thanks for your efforts to save America and put the bad guys away. You’re the right person in the right place at the right time!
Jeff Bridges
https://youtu.be/kcRlZi3V0CQ
One of these State actors was involved: Russia, China or Iran. I think that the DNC may not be behind this. I just watched the 2020 documentary, “Kill Chain: The Cyber War on America’s Elections”. It came out in March this year. The last 30 minutes is scary as hell. We were warned. This may be why AG Barr, the media, our top cyber officials, etc want to kill this story. Our national election may have been hacked by a foreign entity.
Keep up the work Patrick!
Keep up the good work Patrick
Jacob
Thank You, the media, News even Facebook not reporting the truth, they are all covering up for Biden. I am insulted by Trump bashing.
Thank you!
The Senate Judicial Committee left this hearing open until Dec 18th for further submission of evidence and testimony.
Patrick maybe you should contact them and report your experiences
https://youtu.be/oAwMWPzzNgw?t=4354
LOL PB to Rosanna Barr “your not old enough to remember but I am”
She has 10 years on ya
Good interview, bit different than recent ones…. still waiting for Joe Rogan…
ORDER GRANTING EMERGENCY INJUNCTIVE RELIEF
____________________________________________________________________________
THE COURT has before it Plaintiffs’ Emergency Motion for Injunctive Relief filed December
1, 2020, seeking:
1. An order directing the Defendants Wisconsin Elections Commission and Governor Tony
Evers not to certify or to de-certify the 2020 election results in the Presidential and District 3
Congressional races;
2. An order enjoining Defendants from transmitting the currently certified Presidential election
results to the Electoral College;
3. An order requiring Governor Evers to transmit certified Presidential election results that state
that President Donald Trump is the winner of the election;
4. An immediate emergency order to seize and impound all servers, software, voting machines,
tabulators, printers, portable media, logs, ballot applications, ballot return envelopes, ballot images,
Case 2:20-cv-01771-PP Filed 12/01/20 Page 1 of 4 Document 6-1
7
paper ballots, and all “election materials” referenced in Wisconsin Statutes § 9.01(1)(b)11. related to
the November 3, 2020 Wisconsin election for forensic audit and inspection by the Plaintiffs;
5. An order that no votes received or tabulated by machines that were not certified as required
by federal and state law be counted;
https://www.courtlistener.com/recap/gov.uscourts.wied.92717/gov.uscourts.wied.92717.6.1.pdf
Regarding the ORDER GRANTING EMERGENCY INJUNCTIVE RELIEF court filing; it is shown to have been filed by La Crosse County Republican Party Chair Bill Feehan and former 3rd District Congressional candidate Derrick Van Orden, who is also a former Navy SEAL. To be clear and for the record, Mr. Van Orden is on public record stating his name was used without his permission and he is not involved in the lawsuit. It was filed by Sidney Powell using his name. Not sure about Feehan.
That said, I would hope especially given Mr. Van Orden’s background as a SEAL, that he would be extremely interested in overturning a fraudulent election, whether or not he’s involved in that particular lawsuit.
I did not know the back story but there is an order removing him from the suit posted later. But the order halting the certification still stands for now….
Perfect!! Thanks!!
I’m a 8 decades seasoned senior with 23 grands, and 7 greats. My generation has an obligation to get up off of our “I’M ENTITLED” arses, and get engaged. My generation’s silence has made us unwitting partners, in a scheme that ‘s destroying the future for 10s of millions of our kids, grands, and greats. It all began with the 1983 Social Security reform legislation that said “we’ve saved Social Security for the next 75 years”. That set deceit and deception into motion that’s allowed the “GOONS” to steal $2.8 trillion of the people’s retirement dollars. Replace stolen dollars with a government issued Special Obligation Bond (SOB) that they list as an asset on the Social Security trust fund balance sheet. LYING – CHEATING – STEALING – IT’S IN THEIR DNA http://www.americaretoday.com Patrick, America needs you, and folks just like you, who are willing to do what has to be done. TY
Someone rich should put
Roseanne Barr and Candace Owens
together on talk show.
Titled -Not Funny Crap
Let them together expose the shit the media
Attempts to spoon feed US.
That would be an awesome alternative to good morning America (or whatever, I don’t watch tv), kek
You need to put each interview separately.
To avoid scrolling and comments pertaining to each.
I’ve read this information, the Sydney Powell briefs, the court briefings and responses, and I just don’t see any information that can be used as evidence this election is rigged. Like the vote count information. Yes, there are spikes as the vote goes one direction and then the next, but aren’t those pretty necessary for a vote count that moves from one direction to another? This seems like some sort of expert witness BS where “it can’t swing that fast” so something nefarious had to happen. We knew going in Trump wanted everyone to vote in person and the Dems tried to get everyone to vote in advance, preferably not in person (social distancing). So big swings are inevitable. If there was proof of over-voting, it would be a different story, but all of that has been demonstrated as incorrect (wrong precinct, wrong numbers being compared, etc.). At least none of this strikes of most of the noise on this topic which amounts to amateurs complaining because they do not know how elections work. But there still is not any bite in this information so far.
here is a mountain of evidence
https://www.electionevidence.com
A mountain of links … but sadly, none provide any useful evidence
This is exactly correct which is why Trump keeps losing in court. Everyone here is in denial.
Hey @SidneyPowell1 @LLinWood
after seeing the dvs fileshare subdomain for Dominion, I scanned a wildcard “dominionvotingSYSTEMS(.)com” and it led me to a horribly insecure data center in Quanzho, China.
https://mobile.twitter.com/schaumby/status/1328991736425803777
Osama Bin Laden……Obama Joe Biden…….interesting how the letters and the literation coincide. Not a coincidence. There is no coincidence… It is put right out front in our faces…..this is the operation.
Great work! I am sorry the media and the law is unwillingly to recognize the work you have done. This is glaringly obvious as both a researcher and a statistician. In a normal court of law, this would be enough evidence to order an immediate forensic audit, yet our legislature and state officials have neglected their constituents, neglected the law and worst of all, neglected the constitution. It is their duty to do what is right, but corruption is deep at the highest and lowest levels. Thank you again, please keep it up and please don’t give up. This may result in a revolution, taxation without representation. No one is representing their people. NOT ONE to spite your forensic work.
Thanks so much for writing this. I love America and do not want to lose it. I can’t tell much from the graphs and everything but I know the election was rigged. Stacy Abrams has been in GA working on doing that for years and now I guess the Gov, LT Gov and the SOS have been too and they do not even have the decency to resign. Hopefully they will all be charged and we will get to have a new election. Thanks for understanding and telling us all what has been happening.
If anyone is interested here is a picture of the 5 brave patriots whom were killed I can only assume by our own CIA operatives while secure the Scytl server.
I have not confirmed this or found their names yet but I will update and correct as more information is found
https://mobile.twitter.com/SjPolitik/status/1333170014753591297
Wie Sie inzwischen wissen, startete das DoD eine
Razzia auf eine von der CIA betriebene Serverfarm in
Frankfurt, um Server zu sichern, die Beweise fur die
Einmischung der CIA in die Wahlen von 2020 enthalten
(d.h. Hinterturmanipulationen von Wahlergebnissen
Ober Dominion Wahlmaschinen). Jetzt tauchen jedoch
neue lnformationen auf, die darauf hinweisen, dass es
in der Serverfarm-Einrichtung ein Feuergefecht gab, in
das Einheiten der US-Armee-Spezialeinheiten
verwickelt waren, die mit von der CIA ausgebildeten
paramilitarischen Einheiten in Konflikt standen, die aus
Afghanistan eingeflogen wurden, um die Einrichtung zu
verteidigen.
Ein CIA-Offizier wurde bei dem Feuergefecht getotet
und wird nun in den Medien als “in Somalia getotet”
gemeldet. Funf Soldaten der US-Armee wurden
ebenfalls getotet, und es wird erklart, dass sie bei
einem “Hubschrauberabsturz” in Agypten urns Leben
kamen.
Trotz der Todesfalle wurden die Server erfolgreich vom
Verteidigungsministerium sichergestellt, und diese
Server wurden der privaten Geheimdienstgruppe van
Prasident Trump ubergeben, die jetzt Wieder von
General Michael Flynn geleitet wird, der vor kurzem
begnadigt wurde und nun streng geheime
lnformationen verarbeiten dart, da seine
Sicherheitsfreigabe wiederhergestellt wurde.
As you know by now, the DoD started one
Raid on a CIA-operated server farm in
Frankfurt to secure the evidence for the server
CIA interference included in 2020 elections
(i.e. backdoor manipulation of election results
Upper Dominion voting machines). Now diving, however
new information indicating it
There was a gun battle at the server farm facility in
the units of the US Army Special Forces
those involved with being trained by the CIA
paramilitary units that conflicted from
Afghanistan were flown in to the facility too
defend.
A CIA officer was killed in the firefight
and is now in the media as “killed in Somalia”
reported. Five US Army soldiers were there
also killed, and it is stated that they at
killed a “helicopter crash” in Egypt
came.
Despite the death trap, the servers were successfully dated
Defense Ministry ensured, and this
Servers were the private secret service group van
President Trump passed who is now back by
General Michael Flynn is headed recently
was pardoned and now top secret
dart process information as its
Security clearance has been restored.
https://mobile.twitter.com/vinalfano/status/1333177609857937408
Another day, another lawsuit shot down. Not going to well eh Patrick?
Why so smug, eh John? Is it because being one of the useful idiots of the Left prevents you from comprehending the inevitable? Or perhaps your blind hate for Donald Trump and those who stand with him gives you a false sense of security? Honestly, the depth of unhinged hypocrisy in you people is nauseating. Enjoy your brief stay in euphoriatown, because you people overplayed your hand big time.
This Democracy and the freedom she represents will be defended at all costs. COUNT ON IT.
Great work Patrick, i have seen a couple of your interviews. But your interview last nighjt with Redpill78 & M3 was mind blowing especially the part where you siad that evedence collected is a week or two ahead of what has actually been released to the public via patriot media outlets or seen as evidence. Funny how the US Hispanic population understands the dangers of Communism, many having felt the direct implications in the past.You looked tired towards the end interview and i don’t doubt that you ars burning the candle at both ends trying to get this information to the people, so as to keep the Republic and it’s Constitution alive. You will be remembered as an International Hero and Patriot. Unfortunately there isn’t time for you to rest yet, but soon and it will be well deserved, know that many support your great efforts.
I am a Kiwi living in Australia both run by Marxists or caught in a Blackmail trap. I only wish that the two countries that are closest to my heart woudl wake up a little faster from there slumber. My friends and would say my tinfoil hat has been on since the 9/11 wag the dog event. I certainly believe if the US falls the World is lost to the Communists.
Dell Bigtree (The Highwire Bitchute) did a CO2 breathing test on his 11 year old son using multiple masks/bandanas which clearly show a lack of oxygen getting in to the body which are clearly well outside the OHS, Occupational Health and Safety guidelines.
The two dumbest arguements i have heard are from people wearing masks complaining that people not wearing them endanger them. The same as the mRNA vaccine. If you get vaccinated then you’ve done this because you believe it’s going to protect you from Cov/sars 2 otherwise you would not take it. The logical arguement is from the minute we arrive here we get closer to death every day, so if i don’t fear death which is enevitable, and you are protected why do i need to have the jab. Sorry to ramble off topic. I am looking forward to reading your other Exposes. Love from Downunder
Lol that is an impressive combo of 9/11 truther, red scare, anti vax dipshittery. Let me guess, you think the holocaust was fake too?
You’re a wealth of info. Thank you for your moral courage, love of country, and love of our Constitution. We are blessed to have you helping restore our country! I’ll help in any way I can as well!
I’ve not seen anyone make note that over time votes were removed from Trump from one hour to the next. This is shown in the NY Times state count tabulations. This starts in line 272.
From this article: https://www.westernjournal.com/twj-exclusive-viral-memo-changing-trump-legal-strategy/?utm_source=Email&utm_medium=rightalerts&utm_campaign=dailyam&utm_content=ttp&ats_es=5be406bcec59a62f3ee6785288612eb5
See Google Doc: https://docs.google.com/spreadsheets/d/1T_wB66S79FkEDsvUWwRWXSg4Ja-Jx0E4WDNHGmUbvvk/edit?fbclid=IwAR1ljIwtGlPYqOc8xqrd8SbOSjHYN
My heartfelt thanks to you and those that you are supporting to try and get this proof of fraud out! I have NO DOUBT that this fraud occurred – knew it the instant that they said “we are done counting for the day”… and I told my son so at that point when we said “goodnight” and went to sleep.
I agree 100% with your statement that if we allow this MASSIVE FRAUD to stand, we have lost our Great Country. No election will ever be “free and fair” as this election was certainly NEITHER FREE OR FAIR!
Keep up the outstanding work.
Thank you for all your hard work! Keep moving forward!
Good website keeping track of evidence all in one place. Updated as they get it.
https://electionevidence.com/
Can someone please explain to me why the hand recount in GA would not completely rule out “Digital” ballot stuffing?.
Because they printed paper ballots to back up the digital ones. This has been explained in several of the hearings.
Keep fighting. I agree that this country will loose its integrity and we will never have a fair election if this one doesn’t get turned around. We have to keep the integrity of the constitution together. Please work with Trumps legal team even if you are not a Republican we need you.
The New Yorker says, well he wasn’t actually crazy when he talked about Wall Street but now, now he must be crazy about voter fraud… They even bring in a study from Emory U….
Can you send your “friend” at the mag and ask him if he will publicly apologize when all this get proven in the courts?
Awesome investigative skills, and fact reporting…. I think also that VA had something nefarious going on too. They concluded just hours after polling closed for Biden. Very quick decision. Given VA is a purple state, and almost all counties, except the most populous ones, were red this raises a red flag to me….
TJS27
Great interview on Cozy Sunday and good new information. You mentioned crowd strike and DNC hack. You do know that the “hack” was actually Tori of youtube “Tori Says”. She worked for John Brennon’s company and during a normal day as a 3rd party contractor she was asked by her higherups to make a copy of the servers while she was there.
This has all come out in the documentary Shadowgate. https://willardsolomon.com/shadowgate-full-film/ They tie crowd strike and Cambridge analytical directly to CGI Federal and Brennon and Gen Jones. https://www.usaspending.gov/recipient/32b5c106-7349-dfeb-24f2-e2a8f4dbff91-C/latest
Also Patrick Bergy. You really have to watch Shadowgate and contact Tori. I know she can supply information you never dreamed of. She has a lot of the blackmail on our politicians so you can know who the targets of the Dems will be…
If you are already working with him I will feel much better:
https://www.victimoftheswamp.com/home/about/
https://www.freedomstream.tv/tag/patrick-bergy/
Sorry just found your interview with Tori…. EXCELENT!!!
Thank you to you and your team!!!! All you have to do now is to try and be heard,thats nearly impossible with soros controlling every aspect of the media. Why is this man still in our country when he has been kicked out of 6 others?? Beyond belief!! High crimes and treason at best.
What is ‘The DELIAN Project,’ how does it work and how did it effect the 2020 election? Thank you. Keep up the great work.
Thank You for everything. I understand you have health issues. I encourage you to seek out Dr. Shiva Ayyadurai. He knows quite a lot about natural remedies, etc. He did some analysis for Rudy Giuliani on finding the signals for votes in MI and AZ, I believe.
I have Akasha at my will, if I can help you, just ask. [email protected]
Thank you for your work on this Patrick, a man in your position will always have critics but your time at Overstock seems to have hardened you to their ranting ways and for this, I commended you, sir.
The data you present here is strong and seems indisputable. Please keep on this.
It seems that the new youtube censorship is targeting Patrick specifically.
You can not say “wide spread fraud or error” in combination with “that caused Trump to loose” One or the other is okay but in combination they are bad
Patrick, They are blocking the release of the report from the forensic audit: https://www.thelibertybeacon.com/secretary-of-state-blocks-forensic-analysis-of-22-dominion-machines-in-michigan/
If you have this you release it and then tell them to take it up the the Senate J Committee if they have a problem.
Given the Supreme Court decision this evening in the Texas lawsuit it’s time to go scorched earth on these goons. I have faith in your analysis to date, now let it rip.
Can you show the same voting result charts for the last few elections, one year of data could just be a function of how they process election results, especially in the states you show where they process the mail in ballots after the in-person voting, All your “facts” say someone could rig the election nothing shows that it happened.
This is the same type of evidence that has caused countless false sentences…. show me something other than what COULD have happened. “Substitute facts for impressions” you once said these are all impressions.
Get $192 hourly from Google!…Yes this is Authentic since I just got my first payout of $24413 and this was just of a single week… I have also bought my Range Rover Velar right after this payout… It is really cool job I have ever had and you won’t forgive yourself if you do not check it http://www.ps4.cloud/dl/googletrends30
thank you. great job. i knew this had been done but i couldn’t explain it. now i can argue with confidence. i sure hope this helps. this criminal. someone or ones need to go straight to jail. do not pass go & do not collect two hundred dollars. go directly to jail.
https://www.skynews.com.au/details/_6215946537001 you need to get this list
A major leak containing a register with the details of nearly two million CCP members has occurred – exposing members who are now working all over the world, while also lifting the lid on how the party operates under Xi Jinping, says Sharri Markson.
Ms Markson said the leak is a register with the details of Communist Party members, including their names, party position, birthday, national ID number and ethnicity.
Anyone think the crazy thugs that destroyed Stuff in the cities and scared people to move are working for some creep wanting to buy cheap real estate?
Anyone tracking who is buying up real estate?
CCP member list
https://gitlab.com/shanghai-ccp-member-db/shanghai-ccp-member-db/-/raw/master/shanghai-ccp-member.csv
Hi Patrick,
Question about the SolarWinds / Dominion screen capture.
Archive.org picked up that page but shows something different in its history. If it is OK to ask, about when was your page/screen capture taken?
I’m curious if the page is IP/Location sensitive, or when it changed.
At this point I trust you. My motive is more about Archive.org, as I’m never sure how much trust to place in its history and what tampering with it might occur. Just because it says “archive” does not make it so.
Thank you,
Charles
U.S. Treasury, Commerce Depts. Hacked Through SolarWinds Compromise
https://krebsonsecurity.com/2020/12/u-s-treasury-commerce-depts-hacked-through-solarwinds-compromise/
Same SolarWinds????
You are quite right to doubt Archive.org.
I have seen things removed from it, AFTER being archived.
It is just another layer of the Deep State.
Great information and work. What’s next? A Biden presidency is making me ill by the day and although several states submitted divided electoral votes, Mitch McConnell isn’t showing any courage. I’m losing confidence quickly and seeing the future collapse of society.
watching the senate hearings on the elections. The former head of CISA did not say a word about skipping the meeting at DHS. What a tool….
Patrick Bergy
Patrick Byrne
Tori “Says”
Sidney Powell
Lin Wood
All those EXCELLENT people at Allied Security
Does Millie get an exclusive with the group???
I certainly hope you have a historian there to document all of this, this is truly one for History.
You guys need is to get Alan Parrott there to fill in some of the pieces and you could recreate an entire decade of corruption.
Thank you all,
Medals of Freedom for all
Hi Patrick
In regards to the spikes in the graph due to batch loads, Were you able to have the Scanned database queried giving the time these batches were injected and have the data/ballots examined for missing information / fake/blank ballots/ illegal registration etc. This would be Actual data and evidence for the court.
Thanks
Hi Patrick
Regarding the spikes in the charts due to injecting batch loads, was the database queried at the time the data was injected to examine the data/ballots for missing information, fake/invalid ballots, This would be actual data and evidence for the courts which cannot be rejected.
Thanks
Hi Patrick
Regarding the spikes in the charts due to injecting batch loads, was the database queried at the time the data was injected to examine the data/ballots for missing information, fake/invalid ballots, This would be actual data and evidence for the courts.
Thanks
Here is the data I have been collecting: https://docs.google.com/document/d/1eub4niXBw6D2u9pICAwZAgGx-MG_WlvReyRWfeU4Mq0/edit?usp=sharing
Great job, this has taken you many many hours I am sure…
PB should take a look…
God bless you Patrick, praying this election gets reversed it obviously was stolen
Hi Patrick,
Eye opening and very disheartening to know so much evidence exists and our Supreme Court will not act.
Thank you very much for your efforts.
God bless you.
Thanks for the enlightenment. Sad that nothing will ever be done. When corruption is this deep, its too big to fix. The dems knew that- and now we are where we are.
The voting machines used in 2020 election should junked. New machines to be used should be cerfied by the U.S. government, maybe Cyber Command. Any new machine once certified needs to be made tamper proof.
Patrick,
Thanks for all of your work for compiling all of this.
Anyone with an ounce of sense knows this was totally fraudulent. My question is where do we go? It seems no one that could do something about it is interested in hearing about it.
I do hope that January 6th is our reprieve. If some good people in the Senate and congress stand up there may still be hope. But if Biden is ultimately installed, I see no reason for any American to support anything that our government does.
It is important to stay fact based otherwise your work will be susceptible to being labeled that of crazy conspiracy stuff.
The voting irregularities are odd but potentially explainable. For example, there’s never been a president as hated as Pres Trump. The media has been working as propagandists for 4 years. Mail in balloting is a new phenomena. So mathematical models may not have the power they normally would thisntime around.
On the other hand, the one thing that defies logic is how anyone can win 80-99% of super large vote dumps (it is HIGHLY suspicious that it happened in multiple locations and after hours but again, stay fact based). I like the explanation that the software allows supervisors to adjudicate contested votes to a single candidate. This is the 1st real,explanation I’ve ever seen. But the next step…how do you prove that’s what happened?
You are quite right to doubt Archive.org.
I have seen things removed from it, AFTER being archived.
It is just another layer of the Deep State.
When you Listen to SOS Pompeo about the CCP HOW can we the People allow ANY Political Participation of any KIND by our Elected Officials or Government Institutions or our educational Institutions ????? https://youtu.be/Opoko2sNxrU , BOMBSHELL: SolarWinds Owners Have Links to Obama, Clintons, China, Hong Kong and US Election Process https://nworeport.me/2020/12/16/bombshell-solarwinds-owners-have-links-to-obama-clintons-china-hong-kong-and-us-election-process/
Patrick, thank you for all of your hard work on this, and for taking part in the recent White House meetings. Let’s hope something good happens soon for our nation.
P.s. if any readers still take the “Q” nonsense seriously, events of recent days and weeks are More decisive evidence that “Q” and “Q team” are absolute b.s., and MAGA supporters who followed Q have been played as suckers….
If any of the main lines of the”Q” story were true there is zero chance we would be in this predicament on December 21, 2020. Q was always garbage fan fiction for morons.
No grand secret plan, no “we have it all”…. zero comprehensive “military intel” involvement from the beginning….. no masters of the universe in control of how to save the Trump presidency….. no sure plan about what to do now…. Q is garbage. I hate that so many MAGA people were led astray by that Q stuff. Some will say this is a reflection upon Trump and MAGA people as a whole…. but I say the Q phenomenon is mainly an indication of the strong yearning among patriots to see our country saved from truly evil people…. alas, fictionalizing the struggle was never the right way to go.
Patrick Byrne was at White House for 4.5 hour meeting on Friday. He reports,
1) scummy Cippollone and Meadows are trying to ease Trump out of fight plans;
2) leaks to MSM are self interested b.s. (surprise);
3) trust only Rudy and Sydney.
https://www.thegatewaypundit.com/2020/12/betrayed-within-patrick-byrne-blasts-white-house-staff-attending-election-meeting-president-trump-sydney-powell-gen-flynn/
PATRICK BYRNE. YOU SIR ARE A *SHINING STAR* UPON THE DARKEST OF NIGHTS.
They have committed fraud at the highest level and have been caught red handed.
Justice Shall Prevail.
How do we prevail ???.These corrupt governors were guaranteed re election,I’m sure they are guaranteed defence when they sign on Jan 6.As many that are involved (Rep,Dem) I am sure the fix is in even on Jan 6.Maconnel stated that he was hopefull that nobody would contest.In other words (fall in line or else).They have so many weapons on there side i’m sure the governors are not affraid.what can the president do? who can he trust?They keep throughing the constitution in our face,these corrupt people don’t care about the constitution.and now we find that the supreme court is even in on it.VERY CONCEREND! We pray for the President and all that are helping himand us.Thank You, Sember Fi
Thank you Sir! We The People Stand with The Legal President Donald J. Trump! He will not concede! Legally he Wins! God Bless You!
Voting machines got to go. I’m from CANADA and believe that World wide use of voting machines has stolen many elections in North America and world wide! Good to now that Jesus is in Control Yours, Glenn
Patrick you stated you had 2 more bombshells to release, have you done so yet?
He just makes them up. They are not true or fact base.
What can the average citizen do to help, if anything? As a retired LEO it is so very difficult to sit on the sidelines and do NOTHING but wait and watch the corruption unfold.
I know I speak for many when I say that for all intents and purposes it appears as if our hands are tied as the corruption is so deeply ingrained into our government. When our President cannot even trust his advisers, it is indeed a sad state of affairs and shows a direct correlation to the lengths that they will go to achieve whatever they desire as an end result.
So I ask, what, if anything, can be done? And what, if anything, can we, the people who are the victims in this, do to help?
We need the Dominion/Smartmatic voting machines & the ballots forensically investigated. The actual count must be based on legal ballots; then based on legal votes! Great interview with Tracy Beanz
https://www.youtube.com/watch?v=UgeqGmvQXKs&feature=emb_logo
You are all sad anti democracy conspiracy theorists. Trump lost because he is a bad president and a horrible human. If this crazy theory is the case how were the ballots all recounted in Georgia 3 times with the same result? Also, if this stuff is all weak evidence that you could not go to a court of law with because its not fact based. It just makes a bunch of long distance not connected assumptions.
Patrick, sorry to rain on your parade, but this proves nothing.
Why can’t people see that after four years of craziness, criminality, and stupidity, the majority of Americans came to the conclusion that Trump was unfit for office and in over his head. His performance motivated a majority of voting Americans to vote him out. And, the spurts in voting totals that so many seem to think is somehow fraudulent, is just a normal manifestation of the counting of ballots….in-person vote totals and mail-in ballots were tallied at different times. And, oh yes, there was that other elephant in the room: Trump’s response to the coronavirus pandemic. We have 20 percent of the infections and deaths, but only 4 percent of the population….and every thing about Trump’s instincts and response has been proven to be dead-wrong. Remember the “American Resurrection last Easter? How about the bleach/lysol matter. Trump punted on the one “real” crisis he faced. The other crises were those he invented such as the caravan, border wall, etc etc….
Bottom line — the American people have had enough and more than a majority voted against Trump — and the adults still left in American Govt (Barr, Pompeo, etc) have likewise concluded that there was no systemic fraud. May the ghost of Hugo Chavez rest peacefully.
…bravo JoeD….. i think your point have been even further validated by the lawsuits filed by several voting machine co’s that forced several hard right news co’s and Fox to broadcast retractions to their reporting of rampant fraud……time for this silliness to be put away, so glad that DJT was defeated. He was a miserable failure and total unfit for the job.
Dr Byrne,
For the sake of full disclosure, please disclose if you have any ownership in Voatz, Votem, or Medici Venture? If you are questioning the validity of the election, while companies that you have an ownership in are using potential voter fraud as a business case as to why a state, municipality, etc should purchase their blockchain solution, I think it would be important for people to know. Maybe these blockchain voting solutions are the answer, but I think it is only fair for readers to know if there could be any ulterior motives for publicly expressing your voter fraud theories.
He has addressed this many times in the past. He has NO ownership in Overstock, Medici Ventures or any of the companies that Medici has financial interest in. He publicly announced his sale of ALL his stock. He does have a great belief that the companies that he gathered together under Medici while he was Overstock CEO would be great for our country and the world on many many levels. He still supports, at least verbally, all of these ventures and expresses immense confidence in JJ.
As far as I have been able to ascertain, his only financial interest in anything connected to Overstock/Medici is in a purchase, after divesting himself from OSTK, of Ravencoin. Ravencoin is a project supported both developmentally and financially by Medici. BUT Medici has NO ownership in the Ravencoin project and does not directly control the path of the project. Ravencoin was founded like Bitcoin with no owners or centralized control of any kind. I can also tell you that Patrick is over 50% down on his Ravencoin investment at this time. I am quite sure that he has made up that with the rise of BTC.
I will also note your pathetic attempt to ANONYMOULY misdirect and discredit on this subject is quite telling. Your ignorance of publicly available data and the SPIN you put on the misinformation you put in your post shows that you are attempting to subvert the investigation of constitutional violations.
Who are you? What are you hiding? What are your anterior motives?
Lastly thank you for giving me this opportunity to get some news out about Ravencoin. 20 years from now this may prove to be PB’s biggest contribution to our freedom, bigger than what he did concerning Wall St. and bigger than the election. Imagine an economy where the rules are the same for everyone, big or small, and the government can not manipulate or take your livelihood. An economy that allows everyone to reach a world wide market directly WITHOUT Amazon, Itunes, Spodify, Netflix, Youtube, Twitter, Ihart ect…… in the middle. An economy where anyone can take direct payment instantly without a Credit Card company or Bank or other “payment gateway” taking a percentage and holding YOUR earnings for you. Can you visualize a stock market that is easy to understand with no places for manipulation or fraud. Instead of large companies making $100’s of billions off or your advertisement viewing and making $100 of billions more selling your data, data that YOU own, you decide what and when and how your PROPERTY is handled. When I see an advertisement in my web browser I get paid.
All these things are possible now, today. The tools are there already being used. But more support is needed. More companies and individuals need to be using these tools to build their business.
To all of those commenting who really NEED a “smoking gun”…
Why are county election boards REFUSING to hand over voting machines to their state legislatures for a forensic audit? If these elections were as pure as the driven snow, then what is there to hide? All that blather about “protecting voter privacy” is bullshit too. An audit isn’t going to expose who Billy Bob Johnson voted for! It’s about the bigger picture. Only a genuine fool would accept that as an answer.
Watch Ann Vandersteel’s interview with Patrick 12-22-20 on youtube. I caught the last half hour livestreamed so need to go back to watch the video from the beginning. Three bombshells were revealed for which Patrick has a kill switch in case the Deep State punishes him.
Patrick, you need to contact me because I know a good psychic who will read over the phone and let you know if you are in danger.
I’m not quite sure why a “kill switch” would be needed.
Byrne is certainly not the only person who knows these stories, indeed his knowledge probably only goes as far as his source (unless of course he has first-hand knowledge of Epstein’s death, smiley).
Random thought: Was that purported Las Vegas shooter (likely an arms dealer?) involved in Fast & Furious somehow? Probably too Hollywood to be the truth. Real life has more loose ends.
YOU WANT THE BIGGEST “TELL OF ALL”? SIMPLY GO TO THE LEAST TRANSPARENT< BUFOONISH, IN YOUR FACE WE WILL DO ANYTHING YOU WANT" get it "DOMNION OVER ALL OTHER METHODS! LOOK AT THEIR LOCATIONS- well take a gander of a 1983 website done by DOMINION, the HACKS!!
http://www.dominionvoting.cop AND TELL ME YOU WOULD NOT RUN FROM THEM!!
Patrick,
You provide a voice for democracy. Your such an amazing patriot. I’m in my 60’s no and remember the Nixon/ Kennedy election and Mayor Daley’s “influence” (poor choice of words)… more like “come from the grave” voting for Kennedy.
The fraud seen in this 2020 election makes 1960 look like the age of innocence. I shutter to see how the democratic omelet will become. The egg is broken and scrambled alright and the next four years will effect all of our lives. I am in the category of being an Independent voter and this election might remove all voters independence.
You are a hero Patrick and I truly love love you phase to bring Gratefulness Back.. I would love to hear how you look at gratefulness in these times. Bless You and Merry Christmas! Mike
KaMalarkey teh Saiga sez she’ll blow … yor vote away ! https://www.cms.int/sites/default/files/news_featured_image/saiga_navinder_singh.jpg
Patrick,
On behalf of the little guy, deplorables, and regular joes we thank
you for your courageous efforts. It takes a man of extreme intellect
and abilities to take on the global elites. Our country was built on
people like you who capitalized on the American dream and are
willing to sacrifice their character for protecting it. God bless you
and may your efforts here help save the democratic process, integrity
of the election process.
N0 SHIT ! G0BDEM Deep Doo-Doo behind teh BU$H$ !!
C’mon, MAN ! It’s G0BDEM Election FRAUD Epitomized and they ALL Track WI (not shown); but here Ya G0 : https://cdn01.dailycaller.com/wp-content/uploads/2020/11/Wisc-Mich.jpg
Thank you Patrick for a absolutely enlightening report. You are a real patriot. I will be praying for protection for you. Assange needs protection as well. He may seem to be a scoundrel but, I don’t regard him as such. You Sir, are the real deal! Thanks so much for being fearless.God is on the side of truth as you are! Blessings of safety and peace to you.Patricia in Seattle (yuk) Stuck here and never sure what they do with my mail in vote. Thanks for being a patriot and a stand up guy! Tricia p.s. I will try to copy this and send the main body of text to Trump on the White house website.I use!
Seems the Ukrainians have a few Moab’s to drop of their own https://youtu.be/PcOYsmjhTGE
I have been struggling trying to figure out how they got all the people in each of the six counties to make this happen. That is a lot of corrupt people.
After watching this excellent report on the Chinese connections in San Fran and Feinstein I found a piece of it. This report documents the direct connections and funding between CCP, BLM and AFL/CIO. There is a ton of important information in this and all Americans should know these things. https://www.youtube.com/watch?v=1S9YjP5Tfxw
But there is still more. The AFL/CIO provides a lot of infrastructure and BLM provides a lot of malleable emotional new people. After watching this explosive press conference from Ukraine I put it together. After all the Biden stuff they go into the plan for “fixing” the corruption in the Ukrainian “AG” https://youtu.be/PcOYsmjhTGE?t=2860 This is really telling and EVERYONE should watch this part. There is a lot to unpack but you could, and “they” did, use this exact system to generate the kind of workers “they” needed in each county to pull off the fraud. I wonder what data the Unions have on their member???
Gavin Newsom paying almost double for N95 mask to BYD Chinese electric car company.
https://www.politico.com/states/california/story/2020/05/06/newsom-releases-1b-mask-contract-that-reveals-certification-problems-9422887
BYD and Georgia:
https://www.byd.com/sites/Satellite?c=BydArticle&cid=1514428096276&d=Touch&pagename=BYD_EN%2FBydArticle%2FBYD_ENCommon%2FArticleDetails
https://www.redandblack.com/uganews/uga-disputes-electric-bus-contract-controversial-bus-manufacturer-claims-to-have-reached-a-deal/article_04991e22-8aee-11e8-8ae7-df60d75c8f1e.html
http://africa.chinadaily.com.cn/a/201808/15/WS5b74cd96a310add14f386069.html
Patrick — Respect your work and blog posts with the exception that the election was riddled with fraud. Dozens of lawsuits dismissed. Hard Right news networks forced to broadcast retractions of their false/unsubstantiated claims of fraud. I hope that you can further substantiate your claims with tried and true evidence or that you could post a retraction. There hasn’t been fraud. I, for one, am proud our democracy withstood this test and our legal system held firm in these matters. DJT lost. Our country won.
Stop watching mainstream propaganda. The Epoch Times and NewsMax are less biased. I haven’t kept up but last I heard Giuliani and Powell only had three lawsuits and NONE of the evidence was heard. The hundreds of other lawsuits around the country were filed by private citizens, local politicians and election officials. I have no idea what evidence, if any, was heard in those cases either. Most seem to be people protesting their vote was stolen or that they witnessed fraud.
Do you think all judges are honest?
..pam / patrick – suggest strongly that you want the video (happening live now) of the Officials from the State of Georgia Elections very clearly dispute the claims of fraud and specifically the photos that Patrick posted about emergency ballots….. Patrick – he called attn: to your post specifically….it seems that these very intelligent, thorough gov’t officials have done a great job to point out how well the GA election was managed and how fraud did not occur
patrick – the Officials from the GA Elections office specifically spoke of your posting pictures of extra ballots and your claim that this is somehow related to fraud…..be sure you want a recording of this New Conference (happening right now) He also does a GREAT job of supplying real evidence and numbers, verified by different offices w/in the State to prove the false claims by you and DJT and others are just that, not real. Extraordinary claims should be supported by extraordinary evidence. Our elections have been run very, very well. There is no real evidence of fraud, there haven’t been any court filings to support these fake claims of fraudulent voting. The only reason that these fake claims are rising above all the noise is due to DJT.
Can you provide a link, I would like to see what they have to say and provide.
https://www.npr.org/2021/01/04/953321408/georgia-election-official-dont-let-misinformation-suppress-your-own-vote?fbclid=IwAR3BePFegHJJ30iKnjdyW8GFOmFRzSIZGhJ_EO3ufsIDMafakjX_Ie7ZcJg
Hi, Patrick — thanks for all you are doing!! I don’t have a Twatter account but I saw your question about looking for the Jerry Garcia comments on protest and street violence. I think what you want is after 8:00 in this clip, where he talks about “the main asshole” in a crowd who starts violence against police in order to provoke:
https://youtu.be/iN9-kWEcs-I
This is the same ‘market making’ type of ‘software’ control that ‘stabilized’ the markets, right into the 2008 meltdown.
Deciding which company lives or dies, deciding which candidate loses or wins.
Naked shorting America six ways to Sunday.
Circles, spinning around.
Makes you want to find a hill, let it all go and get off the merry go round for good.
Thinking of making a sequel to ‘Where the money went’
Call it ‘where the votes came from’.
https://www.youtube.com/watch?v=YKpmAX_upxk
Another must watch video. The Swiss Post owns the full rights to the software…
hey pb- here is the link to news conf. yesterday in GA where the official spoke specifically to many/all of the bogus claims of fraud made by DJT and his followers. Very intelligent presentation. This official also spoke specifically to your posting of pics from a warehouse showing pallets of ballots that you proposed were evidence of fraud….. I hope you’ll watch it. GA is a particularly good case to study for those claiming fraud in the machine counting of votes since they went through several audits, including HAND counting all the ballots. Amazing how thorough and careful they have been to ensure GA citizens had a free and fair election. One of the things that I notice about your postings is you are thoughtful enough to post corrections/updates when you find compelling and thorough evidence that runs counter to your claims. I truly hope you will watch the news conference plus research other reliable sources and post updates/corrections if warranted
https://www.npr.org/2021/01/04/953321408/georgia-election-official-dont-let-misinformation-suppress-your-own-vote?fbclid=IwAR3BePFegHJJ30iKnjdyW8GFOmFRzSIZGhJ_EO3ufsIDMafakjX_Ie7ZcJg
The issue is that everything involved in the election has to be held for 22 months. This is for the purpose of auditing incase there are questions about the election. Even these “backup” ballots have to be kept for inspection.
52 USC 20701: Retention and preservation of records and papers by officers of elections; deposit with custodian; penalty for violation
Text contains those laws in effect on January 5, 2021
From Title 52-VOTING AND ELECTIONS
Subtitle II-Voting Assistance and Election Administration
CHAPTER 207-FEDERAL ELECTION RECORDS
Jump To:
Source Credit
Miscellaneous
Codification
§20701. Retention and preservation of records and papers by officers of elections; deposit with custodian; penalty for violation
Every officer of election shall retain and preserve, for a period of twenty-two months from the date of any general, special, or primary election of which candidates for the office of President, Vice President, presidential elector, Member of the Senate, Member of the House of Representatives, or Resident Commissioner from the Commonwealth of Puerto Rico are voted for, all records and papers which come into his possession relating to any application, registration, payment of poll tax, or other act requisite to voting in such election, except that, when required by law, such records and papers may be delivered to another officer of election and except that, if a State or the Commonwealth of Puerto Rico designates a custodian to retain and preserve these records and papers at a specified place, then such records and papers may be deposited with such custodian, and the duty to retain and preserve any record or paper so deposited shall devolve upon such custodian. Any officer of election or custodian who willfully fails to comply with this section shall be fined not more than $1,000 or imprisoned not more than one year, or both.
( Pub. L. 86–449, title III, §301, May 6, 1960, 74 Stat. 88 .)
They also did not address the video evidence and did not address it properly in the phone call with Trump.
https://thedonald.win/p/11Rh67Gd8z/wow-ossoff-won-with-5019-of-the-/
Pretty weird.
Hey Patrick, please please don’t take any materials from Ron Watkins and “Neon Revolt” so seriously. They are central figures in the Qookanon world, and their stuff is full of holes. Lin Wood has gone off the deep end with them, too….. please be careful not to harm your own credibility by embracing such characters.
Edward Solomon is reverse engineering an algorithm that has tampered with election results. He is seeing DJT votes flipped to JB. GA at least 25,630; PA at least 124,649; and MI at least 287,980. Unknown culprit (bad actor), but Solomon says, “They built manipulation with cinder blocks. They want you to believe it is natural stone.” This is very complex math, but TRUTH.
https://www.youtube.com/watch?v=qmzbDQy9blg
Paper print outs of the votes. Nobody has been able to explain why election fraud happened when the Georgia hand recount of the paper ballots matched the electronic tally almost perfectly, as did the paper ballot audits in various counties in other states.
For fraud or shredding to have happened, the paper vote tally would not match the electronic tally. But they do.
If fraud happened, the only technical explanation, in light of paper ballot recounts, is for the print outs to NOT have reflected what the voters actually did in the booth. In other words, for the machines to have ignored what the voters pressed and printed out something else instead. But nobody has complained nor seen anything like this. So that didn’t happen.
There are a bunch of fat ladies singing in congress right now
Patrick, nothing from you since last night that I can find. I hope you are helping with the Italy story……is it real? Please let it be and all the Natl Guard being sent to DC are not for Trump Supporters but for the left when the news is broken to them that their victory lap is about to end abruptly.
Patrick, you tweeted about info from voting machines being sent abroad during the GA Senate runoff. We’re lawsuits filed by the GOP immediately?
Hello Patrick! What is going on with Italygate? Is it true? I’ve been trying to find more info about it online- and I’m not finding much. I saw that you posted something about it- and someone reposted it on Parler.
Check nationsinaction.org
Won’t find much there either. Looks like all efforts like this are short of manpower and are unable to post regular updates, giving the sites a dead feel. Sad!
Gab and clouthub not wrong for me , Patrick please post here if you can if we should have hope. Italy?
Where do we follow you now that you have been banned from Twitter?
Patrick,
Thanks for all the information you have shared over the last month. I was relying on you for the truth as the process played itself out. Very disappointed that the truth was not brought forward to the entire nation, the media is just useless, and it feels like a great crime has been allowed to damage this country. Appreciate your efforts and I so wish DJT would have listened to Sidney and you.
Hi, Patrick.
I logged onto Twitter this evening to read your posts, as I usually do, only to find that your account has been suspended. And when I tried to find you on Parler and Minds, the screens just blinked. What a dark day for our country, and the world. Thank you for taking more risks for the rest of us than any one man should, and for being the rare gem that I’ve always known you to be.
A farm is a lovely idea.🌻 I hope you do that. It would be a wonderful place for you to write. I’ll continue to look for your perfect words here.☘
https://www.scrapbook.com/poems/doc/11919.html
Why does Lance Armstrong just keep coming to mind on this.. I mean, 7 Tour de Frances? Give me a break man… Biden did not win without a LOT a doping…
Why are you only complaining when Trump lost? If that was so easy, how could he win in 2016?
Trump broke their algorism in 2016. They were not going to let that happen again. That is why this is so blatant this time. Hillary was guaranteed to win 2016 they didn’t think they had to cheat so offiously.
have a nice day
This didn’t happen over night.
Who were the leaders, the planners, and the truck drivers?
Who put up the money for this coup. Where is the computers that made this happen?
We are indebted to your untiring service to the nation! Thanks for laying all this out in a thorough and understandable fashion. Given your work with Sidney P., I trust this material will be helpful in what I hope will be military tribunals to expeditiously deal with the host of traitors.
Remain safe!
This is garbage and you should be ashamed of yourself
I couldn’t agree more with you.
2020 had an unusual ballot count. I had heard fr years the Kennedy/Nixon election was the high water mark in election turnout, so I thought I would take a look. It appears higher turnout trend started with Bush/Clinton and exploded nce they started running these machines. Kennedy/Nixon had 70 million votes roughly. The USA had 180 million people in 1960. 18, 19 and 20 year olds couldn’t vote, so you might adjust that up 5 million. There were not a significant foreign population in the US then. Today, I venture there are 50 million foreigners. Around 2004, turnout exploded. 2016 was around 130 million, as was 2008. 08 they wanted an Obama landslide. In 2016, they didn’t think Trump would win. Suddenly 2020, counting independents, 160 million. I don’t believe we gave 30 million new citizens and 80% voting age turnout of citizens is off the charts. The first Clinton election was 104 million, but it was fattened by 19 million Perot votes.
https://www.presidency.ucsb.edu/statistics/elections/1988
I suspect, looking at these numbers there has been growing fraud in US elections, likely since the 1980’s. I talk to people and a sizable number could care less about politics. A search says there are 45 million aliens in the US. 330 million minus 45 million is 285 million. Take out about 80 million for kids and felons, that leaves 205 million. 80% don’t turn out. But motor voter and other automatic registration allows them to be accessed. Based on 1960 (I was 5 then and I was aware that election was happening), turnout should be in the 120 million range.
It’s not often that we come across content that really resonates with us, but this one is a standout. From the writing to the visuals, everything is simply wonderful.
Your blog has become a source of guidance and support for me Your words have helped me through some of my toughest moments
This guide was a total lifesaver. The step-by-step approach made everything easy. I appreciate the detail and the clarity. Well done!
https://www.kuailpcvpn.com